一、策略网络
策略函数 π \pi π的输入是状态 s s s和动作 a a a,输出是一个介于0和1之间的概率值,用神经网络 π ( a ∣ s ; θ ) \pi(a \mid s; \boldsymbol{\theta}) π(a∣s;θ)近似策略函数 π ( a ∣ s ) \pi(a\mid s) π(a∣s), θ \bm \theta θ表示神经网络的参数,一开始需要随机初始化,随后利用收集的状态、动作、奖励来更新。
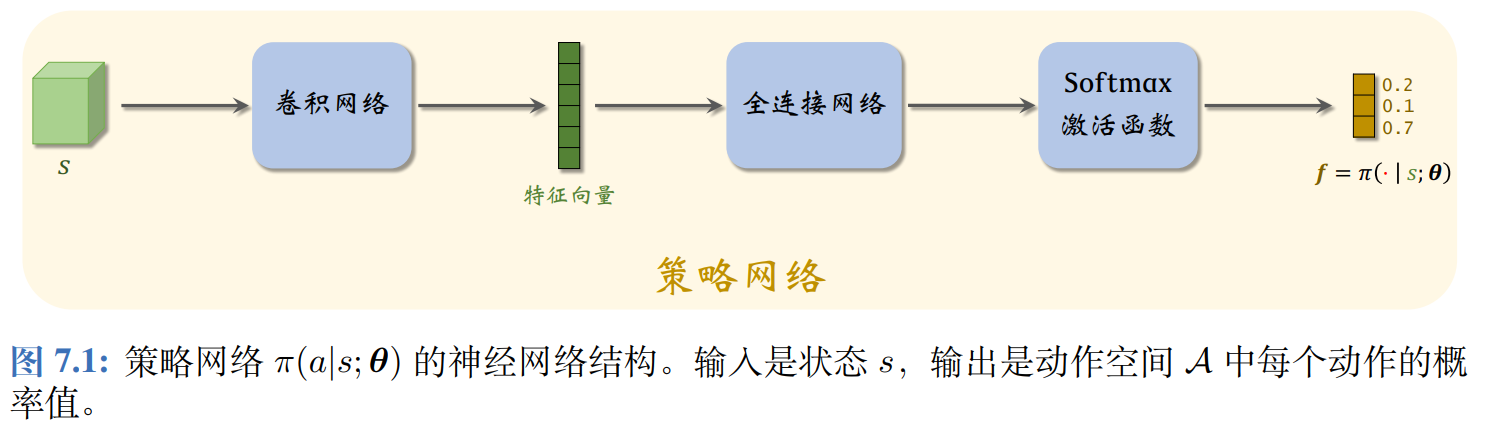
如果一个策略很好,那么对于所有的状态 S S S,那么状态价值 V π ( S ) V_{\pi}(S) Vπ(S)的均值应当很大,因此定义目标函数为:
J ( θ ) = E S [ V π ( S ) ] . J(\theta)=\mathbb{E}_S \left[V_\pi(S) \right]. J(θ)=ES[Vπ(S)].
这个目标函数排除掉了状态 S S S 的因素,只依赖于策略网络 π \pi π 的参数 θ \theta θ;策略越好,则 J ( θ ) J(\theta) J(θ) 越大。所以策略学习可以描述为这样一个优化问题:
max θ J ( θ ) . \max_{\theta} J(\theta). θmaxJ(θ).
其中的策略梯度:
∇ θ J ( θ now ) ≜ ∂ J ( θ ) ∂ θ ∣ θ = θ now \nabla_{\theta} J(\theta_{\text{now}}) \triangleq \left. \frac{\partial J(\theta)}{\partial \theta} \right|_{\theta=\theta_{\text{now}}} ∇θJ(θnow)≜∂θ∂J(θ) θ=θnow
二、策略梯度定理
由于内容比较繁琐,此处不再证明,感兴趣的可以去看相关书籍和论文。
策略梯度定理证明:
∇ θ J ( θ ) = E S [ E A ∼ π ( ⋅ ∣ S ; θ ) [ Q π ( S , A ) ⋅ ∇ θ ln π ( A ∣ S ; θ ) ] ] \nabla_{\theta} J(\theta)=\mathbb{E}_{S} \left[\mathbb{E}_{A \sim \pi(\cdot | S; \theta)} \left[Q_{\pi}(S, A) \cdot \nabla_{\theta} \ln \pi(A | S; \theta) \right] \right] ∇θJ(θ)=ES[EA∼π(⋅∣S;θ)[Qπ(S,A)⋅∇θlnπ(A∣S;θ)]]
每次从环境中观测到一个状态 s s s,它相当于随机变量 S S S 的观测值。然后再根据当前的策略网络(策略网络的参数必须是最新的)随机抽样得出一个动作:
a ∼ π ( ⋅ ∣ s ; θ ) a \sim \pi(\cdot \mid s; \theta) a∼π(⋅∣s;θ)
因为不知道状态 S S S的概率密度函数,所以用蒙特卡洛方法近似策略梯度,来计算随机梯度。
g ( s , a ; θ ) ≜ Q π ( s , a ) ⋅ ∇ θ ln π ( a ∣ s ; θ ) . \boldsymbol{g}(s,a;\boldsymbol{\theta})\quad\triangleq\quad Q_\pi(s,a)\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a|s;\boldsymbol{\theta}). g(s,a;θ)≜Qπ(s,a)⋅∇θlnπ(a∣s;θ).
g ( s , a ; θ ) \boldsymbol{g}(s,a;\boldsymbol{\theta}) g(s,a;θ)是策略梯度 ∇ θ J ( θ ) \nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta}) ∇θJ(θ)的无偏估计:
∇ θ J ( θ ) = E S [ E A ∼ π ( ⋅ ∣ S ; θ ) [ g ( S , A ; θ ) ] ] . \nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta})\quad=\quad\mathbb{E}_S\left[\mathbb{E}_{A\sim\pi(\cdot|S;\boldsymbol{\theta})}\left[\boldsymbol{g}(S,A;\boldsymbol{\theta})\right]\right]. ∇θJ(θ)=ES[EA∼π(⋅∣S;θ)[g(S,A;θ)]].
三、REINFORCE算法
3.1 推导
随机梯度 g ( s , a ; θ ) ≜ Q π ( s , a ) ⋅ ∇ θ ln π ( a ∣ s ; θ ) \boldsymbol{g}(s,a;\boldsymbol{\theta})\quad\triangleq\quad Q_\pi(s,a)\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a|s;\boldsymbol{\theta}) g(s,a;θ)≜Qπ(s,a)⋅∇θlnπ(a∣s;θ)中的动作价值函数 Q π Q_\pi Qπ是未知的,导致无法直接计算 g ( s , a ; θ ) \boldsymbol{g}(s,a;\boldsymbol{\theta}) g(s,a;θ),REINFORCE 进一步对 Q π Q_\pi Qπ做蒙特卡洛近似,把它替换成回报 u u u,用实际观测的回报近似 Q π Q_\pi Qπ
动作价值函数定义为 U t U_t Ut 的条件期望:
Q π ( s t , a t ) = E [ U t ∣ S t = s t , A t = a t ] Q_\pi(s_t,a_t)=\mathbb{E}\left[U_t|S_t=s_t,A_t=a_t\right] Qπ(st,at)=E[Ut∣St=st,At=at]
因为 u t u_t ut是随机变量 U t U_t Ut的观测值,所以 u t u_t ut是上面公式中期望的蒙特卡洛近似。在实践中,可以用 u t u_t ut代替 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at),那么随机梯度 g ( s t , a t ; θ ) \boldsymbol{g}(s_t,a_t;\boldsymbol{\theta}) g(st,at;θ)可以近似成:
g ~ ( s t , a t ; θ ) = u t ⋅ ∇ θ ln π ( a t ∣ s t ; θ ) \tilde{\boldsymbol{g}}(s_t,a_t;\boldsymbol{\theta})=u_t\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a_t|s_t;\boldsymbol{\theta}) g~(st,at;θ)=ut⋅∇θlnπ(at∣st;θ)
g ~ \tilde{\boldsymbol{g}} g~是 g \boldsymbol{g} g的无偏估计,所以也是策略梯度 ∇ θ J ( θ ) \nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta}) ∇θJ(θ)的无偏估计; g ~ \tilde{\boldsymbol{g}} g~也是一种随机梯度。
3.2 REINFORCE算法训练流程
假设当前策略网络的参数是 θ n o w \theta_{\mathrm{now}} θnow,REINFORCE 执行下面的步骤对策略网络的参数做一次更新:
(1)用策略网络 θ n o w \theta_{\mathrm{now}} θnow控制智能体从头开始玩一局游戏,得到一条轨迹 (Trajectory):
s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , ⋯ , s n , a n , r n . s_1,a_1,r_1,\quad s_2,a_2,r_2,\quad\cdots,\quad s_n,a_n,r_n. s1,a1,r1,s2,a2,r2,⋯,sn,an,rn.
(2)计算所有的回报:
u t = ∑ k = t n γ k − t ⋅ r k , ∀ t = 1 , ⋯ , n . u_t=\sum_{k=t}^n\gamma^{k-t}\cdot r_k,\quad\forall t=1,\cdots,n. ut=k=t∑nγk−t⋅rk,∀t=1,⋯,n.
(3)用 { ( s t , a t ) } t = 1 n \{(s_t,a_t)\}_{t=1}^n {(st,at)}t=1n作为数据,做反向传播计算:
∇ θ ln π ( a t ∣ s t ; θ n o w ) , ∀ t = 1 , ⋯ , n . \nabla_{\boldsymbol{\theta}}\ln\pi(a_t\mid s_t;\boldsymbol{\theta}_{\mathrm{now}}),\quad\forall t=1,\cdots,n. ∇θlnπ(at∣st;θnow),∀t=1,⋯,n.
(4)做随机梯度上升更新策略网络参数:
θ n e w ← θ n o w + β ⋅ ∑ t = 1 n γ t − 1 ⏟ 严格推导时,需要这个参数 ⋅ u t ⋅ ∇ θ ln π ( a t ∣ s t ; θ n o w ) ⏟ 即随机梯度 g ~ ( s t , a t ; θ n o w ) . \boldsymbol{\theta_\mathrm{new}} \leftarrow \boldsymbol{\theta_\mathrm{now}} + \beta \cdot \sum_{t=1}^n \underbrace {\gamma^{t-1}}_ {\text{严格推导时,需要这个参数}}\cdot \underbrace{u_t \cdot \nabla_{\boldsymbol{\theta}}\ln\pi\big(a_t\big| s_t;\boldsymbol{\theta_\mathrm{now}}\big)}_{\text{即随机梯度 }\tilde{\boldsymbol{g}}(s_t,a_t;\boldsymbol{\theta_\mathrm{now}})} . θnew←θnow+β⋅t=1∑n严格推导时,需要这个参数 γt−1⋅即随机梯度 g~(st,at;θnow) ut⋅∇θlnπ(at st;θnow).
四、actor-critic网络
4.1 价值网络
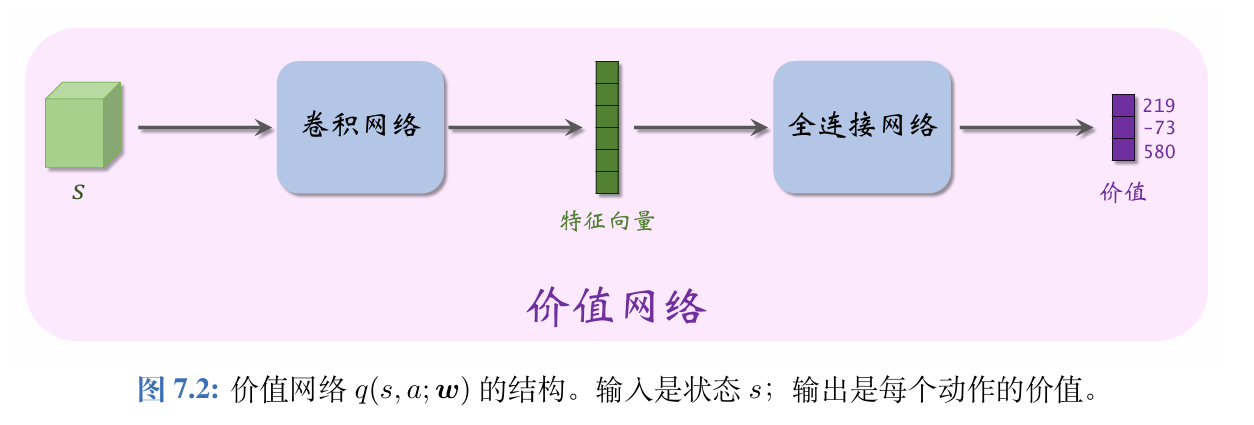
Actor-Critic 方法中用一个价值网络 q ( s , a ; w ) q(s,a;\boldsymbol{w}) q(s,a;w)近似动作价值函数 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a),其中的 w \boldsymbol{w} w表示神经网络中可训练的参数。
虽然价值网络 q ( s , a ; w ) q(s,a;\boldsymbol{w}) q(s,a;w)与之前学的DQN有相同的结构,但是两者的意义不同,训练算法也不同。
1、价值网络是对动作价值函数 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a)的近似。而 DQN 则是对最优动作价值函数 Q ⋆ ( s , a ) Q_\star(s,a) Q⋆(s,a) 的近似。
2、对价值网络的训练使用的是SARSA算法,它属于同策略,不能用经验回放。对DQN的训练使用的是Q学习算法,它属于异策略,可以用经验回放。
4.2 算法推导
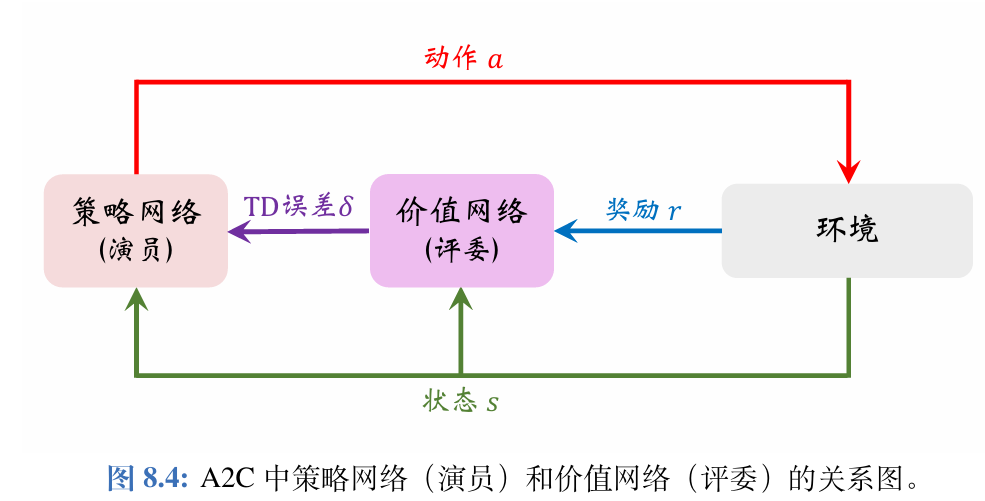
以下是Actor-Critic 方法中策略网络(演员)和价值网络(评委)的关系图。
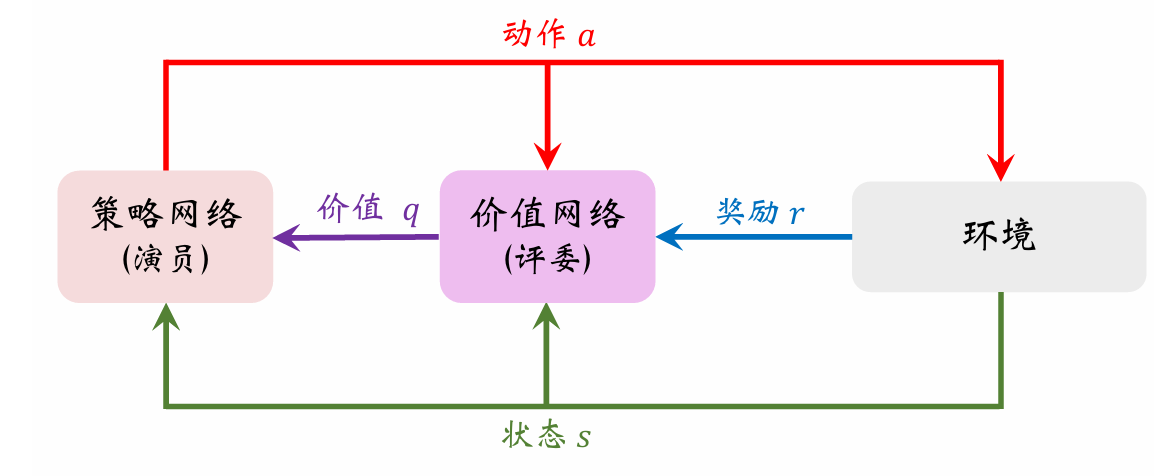
Actor-Critic 翻译成“演员—评委”方法。策略网络 π ( a ∣ s ; θ ) \pi(a|s;\boldsymbol{\theta}) π(a∣s;θ)相当于演员,它基于状
态 s s s做出动作 a a a。价值网络 q ( s , a ; w ) q(s,a;\boldsymbol{w}) q(s,a;w)相当于评委,它给演员的表现打分,评价在状态 s s s的情况下做出动作 a a a的好坏程度。
为什么不直接把奖励R反馈给策略网络(演员),而要用价值网络(评委)这样一个中介呢?
策略学习的目标函数 J ( θ ) J(\boldsymbol{\theta}) J(θ)是回报 U U U的期望,而不是奖励R的期望;注意回报U和奖励 R R R的区别。虽然能观测到当前的奖励 R R R,但是它对策略网络是毫无意义的;训练策略网络(演员)需要的是回报 U U U,而不是奖励 R R R。价值网络(评委)能够估算出回报 U U U的期望,因此能帮助训练策略网络(演员)。
4.2.2 训练价值网络(评委)
训练策略网络的基本想法是用策略梯度 ∇ θ J ( θ ) \nabla_{\boldsymbol{\theta}}J(\boldsymbol{\theta}) ∇θJ(θ)的近似来更新参数 θ \boldsymbol{\theta} θ.
由之前总结出的策略梯度的无偏估计:
g ( s , a ; θ ) ≜ Q π ( s , a ) ⋅ ∇ θ ln π ( a ∣ s ; θ ) . \boldsymbol{g}(s,a;\boldsymbol{\theta})\triangleq Q_\pi\left(s,a\right)\cdot\nabla_{\boldsymbol{\theta}}\ln\pi\left(a|s;\boldsymbol{\theta}\right). g(s,a;θ)≜Qπ(s,a)⋅∇θlnπ(a∣s;θ).
其中,因为价值网络 q ( s , a ; w ) q(s,a;\boldsymbol{w}) q(s,a;w)是对动作价值函数 Q π ( s , a ) Q_{\pi}(s,a) Qπ(s,a)的近似,所以把上面公式中的 Q π Q_{\pi} Qπ替换成价值网络,得到近似策略梯度:
g ^ ( s , a ; θ ) ≜ q ( s , a ; w ) ⏟ 评委的打分 ⋅ ∇ θ ln π ( a ∣ s ; θ ) . \widehat{\boldsymbol{g}}(s,a;\boldsymbol{\theta})\quad\triangleq\quad\underbrace{q(s,a;\boldsymbol{w})}_\text{评委的打分}\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a\mid s;\boldsymbol{\theta}). g (s,a;θ)≜评委的打分 q(s,a;w)⋅∇θlnπ(a∣s;θ).
最后做梯度上升更新策略网络的参数:
θ ← θ + β ⋅ g ^ ( s , a ; θ ) . \boldsymbol{\theta}\leftarrow\boldsymbol{\theta}+\beta\cdot\widehat{\boldsymbol{g}}(s,a;\boldsymbol{\theta}). θ←θ+β⋅g (s,a;θ).
4.2.1 用目标网络改进训练
- 观测到当前状态 s t s_{t} st,根据策略网络做决策: a t ∼ π ( ⋅ ∣ s t ; θ n o w ) a_t\sim\pi(\cdot\mid s_t;\boldsymbol{\theta}_\mathrm{now}) at∼π(⋅∣st;θnow),并让智能体执行动作 a t a_{t} at。
- 从环境中观测到奖励 r t r_t rt和新的状态 s t + 1 s_{t+1} st+1。
- 根据策略网络做决策: a ~ t + 1 ∼ π ( ⋅ ∣ s t + 1 ; θ n o w ) \tilde{a}_{t+1}\sim\pi(\cdot\mid s_{t+1};\boldsymbol{\theta}_{\mathrm{now}}) a~t+1∼π(⋅∣st+1;θnow),但是不让智能体执行动作 a ~ t + 1 \tilde{a}_{t+1} a~t+1
- 让价值网络给 ( s t , a t ) (s_{t},a_{t}) (st,at)打分:
q t ^ = q ( s t , a t ; w n o w ) . \widehat{q_t}=q\left(s_t,a_t;\boldsymbol{w}_\mathrm{now}\right). qt =q(st,at;wnow). - 让目标网络给 ( s t + 1 , a ~ t + 1 ) (s_{t+1},\tilde{a}_{t+1}) (st+1,a~t+1) 打分:
q t + 1 ^ = q ( s t + 1 , a ~ t + 1 ; w n o w − ) \widehat{q_{t+1}}=q\left(s_{t+1},\tilde{a}_{t+1};\boldsymbol{w}_{\mathrm{now}}^-\right) qt+1 =q(st+1,a~t+1;wnow−) - 计算TD目标和TD误差:
y t ^ = r t + γ ⋅ q t + 1 ^ 和 δ t = q t ^ − y t ^ . \widehat{y_t}=r_t+\gamma\cdot\widehat{q_{t+1}}\quad\text{ 和 }\quad\delta_t=\widehat{q_t}-\widehat{y_t}. yt =rt+γ⋅qt+1 和 δt=qt −yt . - 更新价值网络:
w n e w ← w n o w − α ⋅ δ t ⋅ ∇ w q ( s t , a t ; w n o w ) . \boldsymbol{w}_{\mathrm{new~}}\leftarrow\boldsymbol{w}_{\mathrm{now~}}-\alpha\cdot\delta_{t}\cdot\nabla_{\boldsymbol{w}}q\left(s_{t},a_{t};\boldsymbol{w}_{\mathrm{now}}\right). wnew ←wnow −α⋅δt⋅∇wq(st,at;wnow). - 更新策略网络:
θ n e w ← θ n o w + β ⋅ q ^ t ⋅ ∇ θ ln π ( a t ∣ s t ; θ n o w ) \boldsymbol{\theta}_{\mathrm{new}}\leftarrow\boldsymbol{\theta}_{\mathrm{now}}+\beta\cdot\widehat{q}_{t}\cdot\nabla_{\boldsymbol{\theta}}\ln\pi \begin{pmatrix} a_{t}|s_{t};\boldsymbol{\theta}_{\mathrm{now}} \end{pmatrix} θnew←θnow+β⋅q t⋅∇θlnπ(at∣st;θnow) - 设 τ ∈ ( 0 , 1 ) \tau\in(0,1) τ∈(0,1)是需要手动调的超参数。做加权平均更新目标网络的参数:
w n e w − ← τ ⋅ w n e w + ( 1 − τ ) ⋅ w n o w − w_{\mathrm{new}}^-\leftarrow\tau\cdot w_{\mathrm{new}}+ \begin{pmatrix} 1-\tau \end{pmatrix}\cdot\boldsymbol{w}_{\mathrm{now}}^- wnew−←τ⋅wnew+(1−τ)⋅wnow−
五、带基线的策略梯度方法
(过多公式,此处不再推导)
1、在策略梯度中加入基线可以减小方差,显著提升实验效果,实践中常用 b = V π ( S ) b=V_{\pi}(S) b=Vπ(S)作为基线(不依赖于动作 A A A)
2、可以用基线来改进REINFORCE算法,价值网络 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w)近似状态价值函数 V π ( S ) V_{\pi}(S) Vπ(S),把 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w)作为基线,用策略梯度上升来更新策略网络 π ( a ∣ s ; θ ) \pi(a|s;\boldsymbol{\theta}) π(a∣s;θ),用蒙特卡洛方法(而非自举)来更新价值网络 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w)。
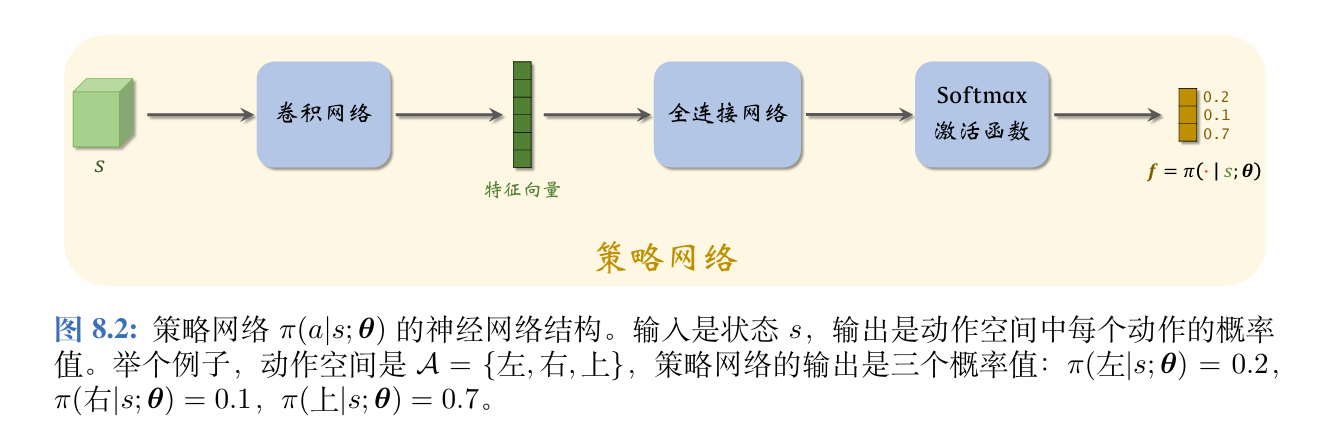
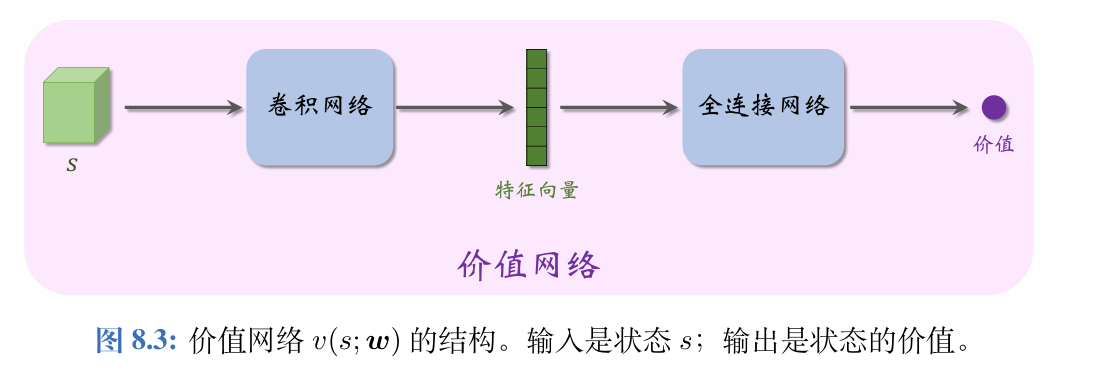
带基线的REINFORCE算法中,此处的价值网络 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w)与之前使用的价值网络 q ( s , a ; w ) q(s,a;\boldsymbol{w}) q(s,a;w)区别较大。此处的 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w)是对状态价值 V π V_{\pi} Vπ的近似,而非对动作价值 Q π Q_{\pi} Qπ的近似。 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w)的输入是状态 s s s,输出是一个实数,作为基线。策略网络和价值网络的输入都是状态 s s s,因此可以让两个神经网络共享卷积网络的参数,这是编程实现中常用的技巧。
虽然带基线的 REINFORCE 有一个策略网络和一个价值网络,但是这种方法不是Actor-Critic。价值网络没有起到“评委”的作用,只是作为基线而已,目的在于降低方差,加速收敛。真正帮助策略网络(演员)改进参数 θ \boldsymbol{\theta} θ(演员的演技)的不是价值网络,而是实际观测到的回报 u u u。
3、用基线方法改进的 Actor-Critic得到的方法叫做 Advantage Actor-Critic (A2C)
它也有一个策略网络 π ( a ∣ s ; θ ) \pi(a|s;\boldsymbol{\theta}) π(a∣s;θ)和一个价值网络 v ( s ; w ) v(s;\boldsymbol{w}) v(s;w),用策略梯度上升来更新策略网络,用TD算法来更新价值网络。
六、策略学习的高级技巧
6.1 置信域策略优化
置信域策略优化(TrustRegionPolicyOptimization,TRPO)是一种策略学习方法,。跟策略梯度方法相比,TRPO有两个优势:第一,TRPO表现更稳定,收敛曲线不会剧烈波动,而且对学习率不敏感;第二,TRPO用更少的经验(即智能体收集到的状态、动作、奖励)就能达到与策略梯度方法相同的表现。
置信域方法需要构造一个函数 L ( θ ∣ θ now ) L\left(\boldsymbol{\theta} \mid \boldsymbol{\theta}_{\text {now }}\right) L(θ∣θnow ) 很接近 J ( θ ) , ∀ θ ∈ N ( θ now ) J(\boldsymbol{\theta}), \quad \forall \boldsymbol{\theta} \in \mathcal{N}\left(\boldsymbol{\theta}_{\text {now }}\right) J(θ),∀θ∈N(θnow ),那么集合 N ( θ now ) \mathcal{N}\left(\boldsymbol{\theta}_{\text {now }}\right) N(θnow )就被称为置信域。在 θ now \boldsymbol{\theta}_{\text {now }} θnow 的邻域中,可以信任 L ( θ ∣ θ now ) L\left(\boldsymbol{\theta} \mid \boldsymbol{\theta}_{\text {now }}\right) L(θ∣θnow ) ,用它来替代目标函数 J ( θ ) J(\boldsymbol{\theta}) J(θ)
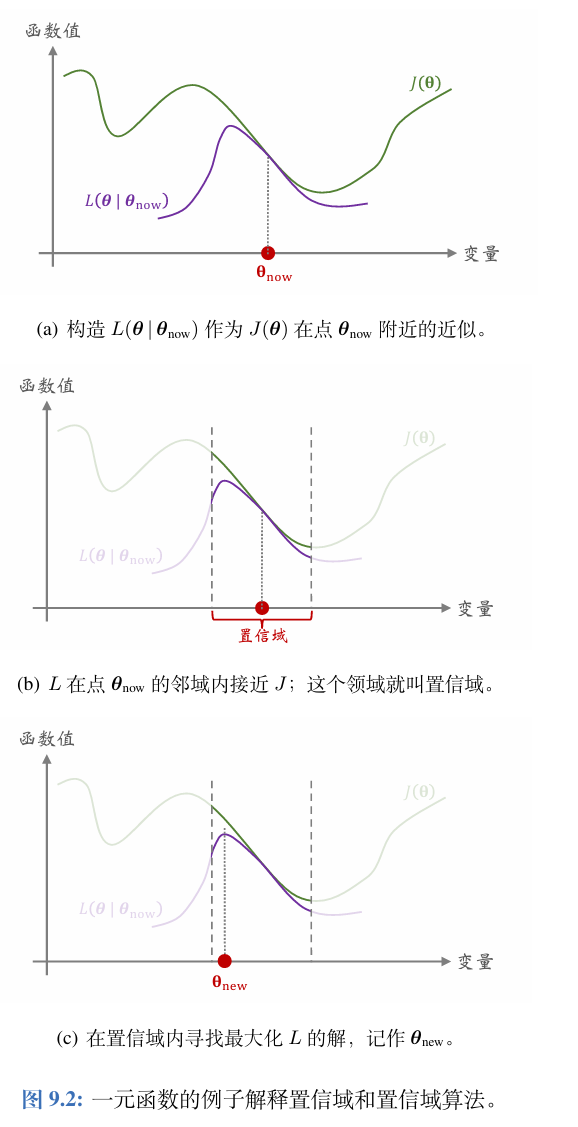
第一步——做近似: 给定 θ now \boldsymbol{\theta}_{\text {now }} θnow ,构造函数 L ( θ ∣ θ now ) L\left(\boldsymbol{\theta} \mid \boldsymbol{\theta}_{\text {now }}\right) L(θ∣θnow ),使得
对于所有的 θ ∈ N ( θ now ) \boldsymbol{\theta} \in \mathcal{N}\left(\boldsymbol{\theta}_{\text {now }}\right) θ∈N(θnow ),函数值 L ( θ ∣ θ now ) L\left(\boldsymbol{\theta} \mid \boldsymbol{\theta}_{\text {now }}\right) L(θ∣θnow )与 J ( θ ) J(\boldsymbol{\theta}) J(θ) 足够接近。
第二步——最大化: 在置信域 N ( θ now ) \mathcal{N}\left(\boldsymbol{\theta}_{\text {now }}\right) N(θnow ) 中寻找变量 θ \boldsymbol{\theta} θ的值,
使得函数 L L L的值最大化。把找到的值记作:
θ n e w = argmax θ ∈ N ( θ n o w ) L ( θ ∣ θ n o w ) \boldsymbol{\theta}_\mathrm{new~}=\underset{\boldsymbol{\theta}\in\mathcal{N}(\boldsymbol{\theta}_\mathrm{now})}{\operatorname*{\operatorname*{argmax}}}L(\boldsymbol{\theta}\mid\boldsymbol{\theta}_\mathrm{now}) θnew =θ∈N(θnow)argmaxL(θ∣θnow)
1、置信域方法指的是一大类数值优化算法,通常用于求解非凸问题,对于一个最大化问题,算法重复两个步骤——做近似,最大化,直到算法收敛。
2、置信域策略优化(TRPO)是一种置信域方法,它的目标是最大化目标函数 J ( θ ) = E S [ V π ( S ) ] J(\boldsymbol{\theta})=\mathbb{E}_S\left[V_\pi(S)\right] J(θ)=ES[Vπ(S)],与策略梯度算法相比,TRPO的优势在于更稳定以及用更少的样本即可达到收敛。
6.2 策略学习中的熵正则(EntropyRegularization)
我们希望策略网络的输出的概率不要集中在一个动作上,至少要给其他的动作一些非零的概率,让这些动作能被探索到。可以用熵(Entropy)来衡量概率分布的不确定性。
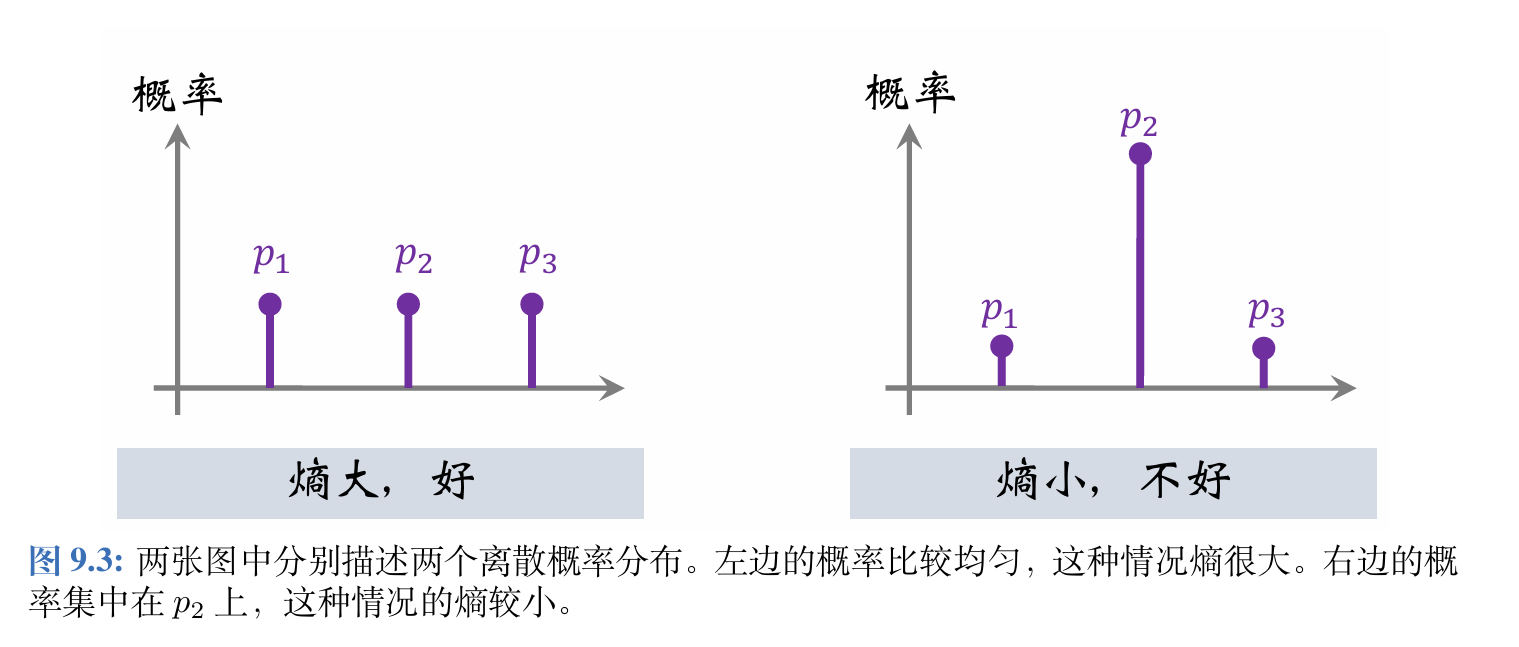
对于上述离散概率分布 p = [ p 1 , p 2 , p 3 ] \boldsymbol{p}=[p_1,p_2,p_3] p=[p1,p2,p3],熵等于:
Entropy ( p ) = − ∑ i = 1 3 p i ⋅ ln p i \begin{aligned} \operatorname{Entropy}(\boldsymbol{p})=-\sum_{i=1}^3p_i\cdot\ln p_i \end{aligned} Entropy(p)=−i=1∑3pi⋅lnpi
熵小说明概率质量很集中,熵大说明随机性很大。
把熵作为正则项,放到策略学习的目标函数中,动作空间离散概率分布的熵定义为:
H ( s ; θ ) ≜ E n t r o p y [ π ( ⋅ ∣ s ; θ ) ] = − ∑ a ∈ A π ( a ∣ s ; θ ) ⋅ ln π ( a ∣ s ; θ ) . H(s;\boldsymbol{\theta})\triangleq\mathrm{~Entropy~}\left[\pi(\cdot|s;\boldsymbol{\theta})\right]=-\sum_{a\in\mathcal{A}}\pi(a|s;\boldsymbol{\theta})\cdot\ln\pi(a|s;\boldsymbol{\theta}). H(s;θ)≜ Entropy [π(⋅∣s;θ)]=−a∈A∑π(a∣s;θ)⋅lnπ(a∣s;θ).
熵 H ( s ; θ ) H(s;\boldsymbol{\theta}) H(s;θ)只依赖于状态 s s s与策略网络参数 θ \boldsymbol{\theta} θ。希望对于大多数的状态 s s s,熵会比较大,也就是让 E S [ H ( S ; θ ) ] \mathbb{E}_S[H(S;\boldsymbol{\theta})] ES[H(S;θ)]比较大。
策略学习的目标函数是 J ( θ ) = E S [ V π ( S ) ] J(\boldsymbol{\theta})=\mathbb{E}_{S}[V_{\pi}(S)] J(θ)=ES[Vπ(S)],策略学习的目的是寻找参数 θ \boldsymbol{\theta} θ使得 J ( θ ) J(\boldsymbol{\theta}) J(θ)最大化,同时,还希望让熵比较大,所以把熵作为正则项,放到目标函数里。
使用熵正则的策略学习可以写作这样的最大化问题:
max θ J ( θ ) + λ ⋅ E S [ H ( S ; θ ) ] . \max_\theta J(\boldsymbol{\theta})+\lambda\cdot\mathbb{E}_S\left[H\left(S;\boldsymbol{\theta}\right)\right]. θmaxJ(θ)+λ⋅ES[H(S;θ)].
策略学习中常用熵正则这种技巧,即鼓励策略网络输出的概率分布有较大的熵,熵越大,概率分布越均匀;熵越小,概率质量越集中在少数动作上。
七、连续控制
7.1 连续空间的离散化
如果把连续动作空间做离散化,那么离散控制的方法就能直接解决连续控制问题。
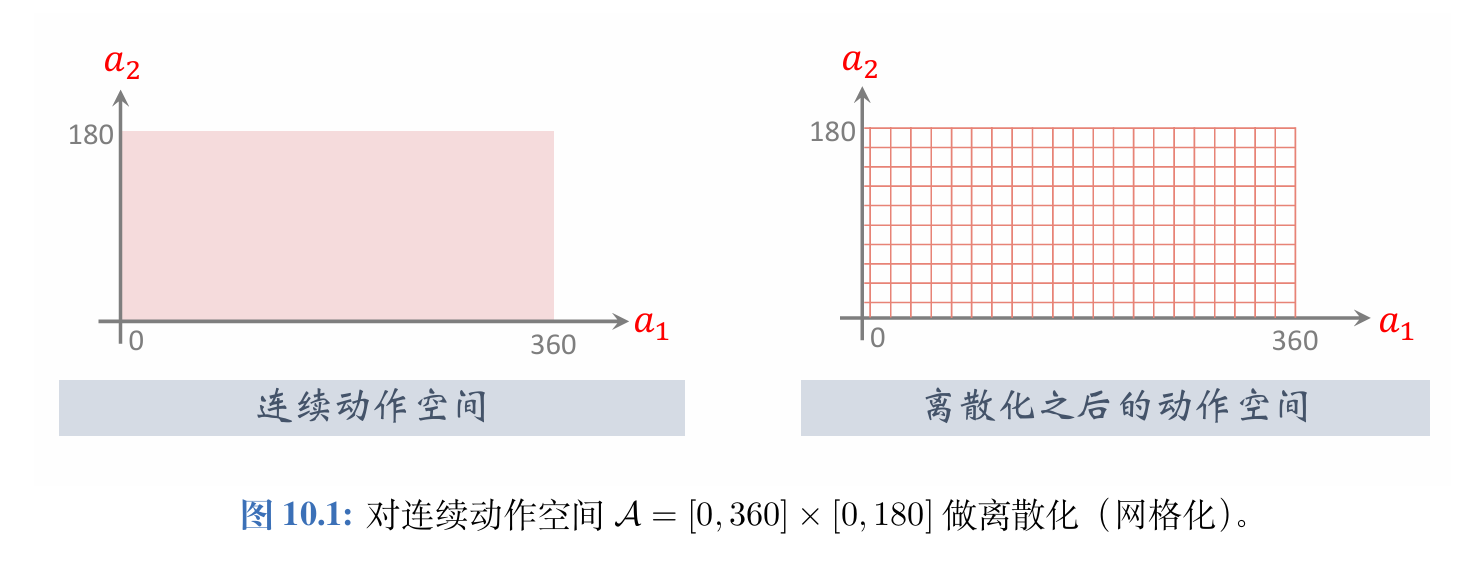
如果要把此前学过的离散控制方法应用到连续控制上,必须要对连续动作空间做离散化(网格化)。
把自由度记作 d d d。自由度 d d d 越大,网格上的点就越多,而且数量随着 d d d 指数增长,会造成维度灾难。动作空间的大小即网格上点的数量。如果动作空间太大,DQN和策略网络的训练都变得很困难,强化学习的结果会不好。上述离散化方法只适用于自由度 d d d 很小的情况;如果 d d d 不是很小,就应该使用连续控制方法。后面两节介绍两种连续控制的方法。
7.2 DDPG
深度确定策略梯度(Deep Deterministic Policy Gradient, DDPG)) 是最常用的连续控制方法。
{ “深度”:说明使用深度神经网络 “确定性”:说明输出是确定性的动作 “策略梯度”:说明使用策略梯度学习策略网络 \begin{cases} “深度”:说明使用深度神经网络\\ “确定性”:说明输出是确定性的动作\\ “策略梯度”:说明使用策略梯度学习策略网络 \end{cases} ⎩ ⎨ ⎧“深度”:说明使用深度神经网络“确定性”:说明输出是确定性的动作“策略梯度”:说明使用策略梯度学习策略网络
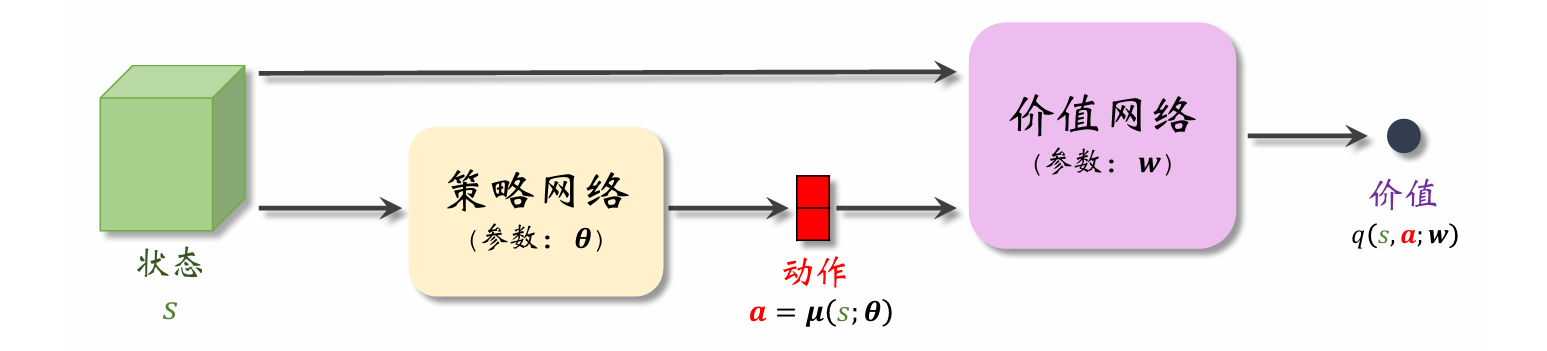
DDPG是一种Actor-Critic 方法,它有一个策略网络(演员),一个价值网络(评委)。策略网络控制智能体做运动,它基于状态 s s s做出动作 a a a。价值网络不控制智能体,只是基于状态 s s s 给动作 a a a打分,从而指导策略网络做出改进。
DDPG的策略网络不同于Actor-Critic的策略网络:
Actor-Critic中的策略网络 π ( a ∣ s ; θ ) \pi(a|s;\boldsymbol{\theta}) π(a∣s;θ)带有随机性:给定状态 s s s,策略网络输出的是离散动作空间 A \mathcal A A上的概率分布; A \mathcal A A中的每个元素(动作)都有一个概率值。智能体依据概率分布,随机从 A \mathcal A A中抽取一个动作,并执行动作。
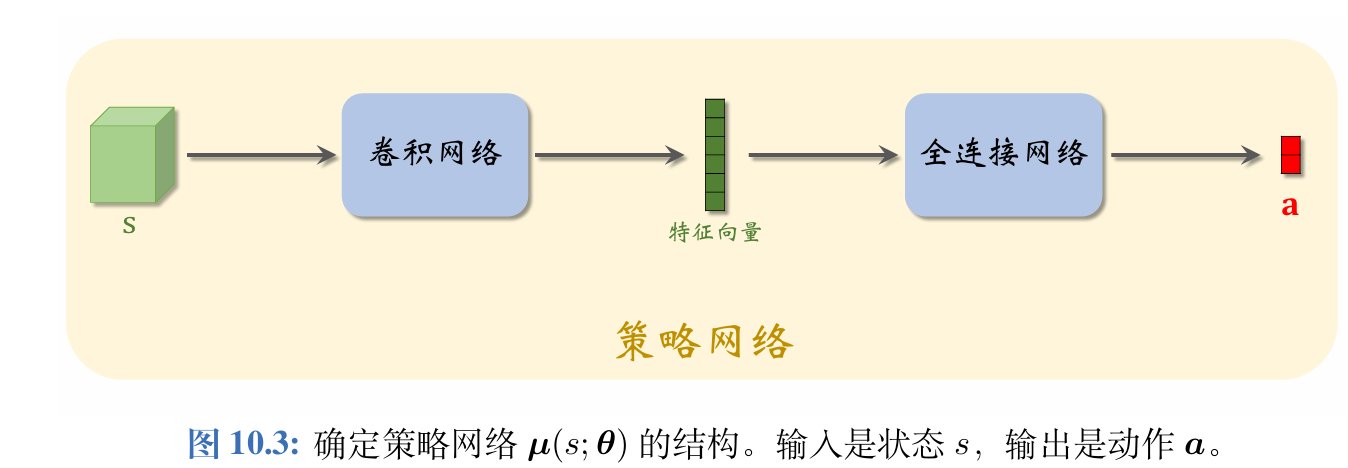
而DDPG的确定策略网络 a = μ ( s ; θ ) a=\boldsymbol{\mu}(s;\boldsymbol{\theta}) a=μ(s;θ)没有随机性:对于确定的状态 s s s,策略网络 μ \boldsymbol{\mu} μ输出的动作 a a a是确定的。动作 a a a直接是 μ \boldsymbol{\mu} μ的输出,而非随机抽样得到的。
DDPG的价值网络 q ( s , a ; w ) q(s,\boldsymbol{a};\boldsymbol{w}) q(s,a;w)是对动作价值函数 Q π ( s , a ) Q_{\pi}(s,\boldsymbol{a}) Qπ(s,a)的近似。
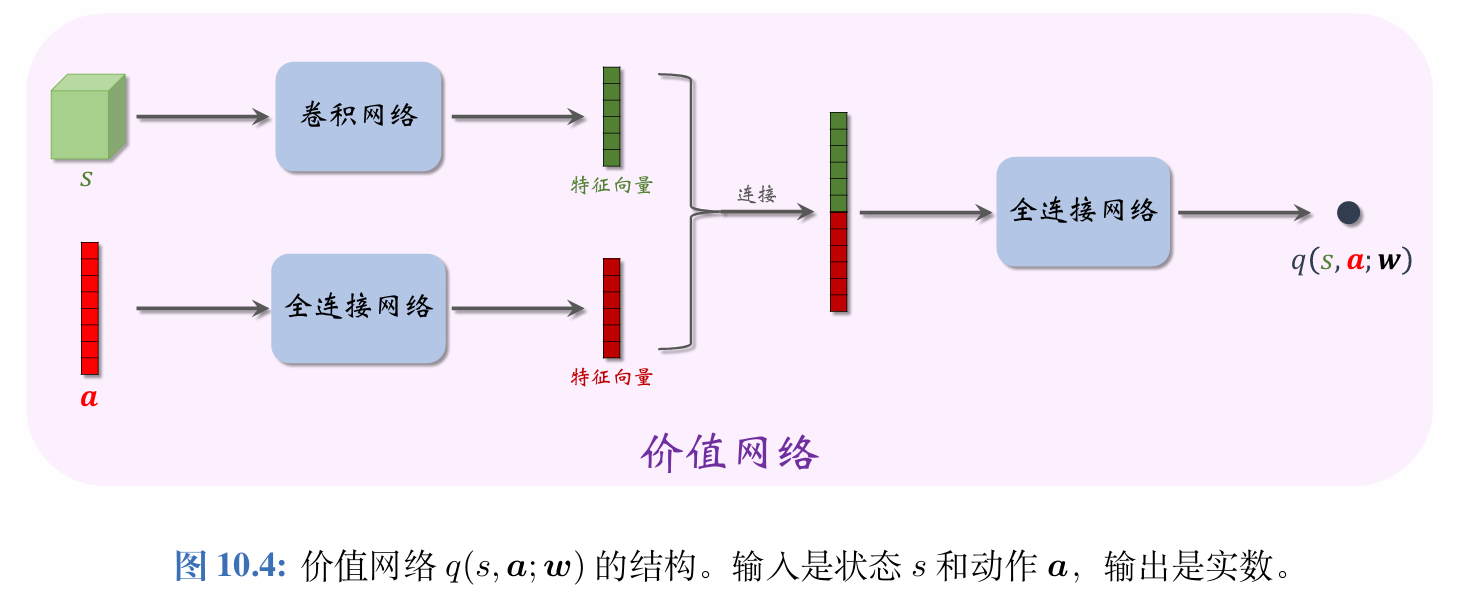
在训练的过程中,价值网络帮助训练策略网络;在训练结束之后,价值网络就被丢弃,由策略网络控制智能体。
7.3 TD3算法
由于存在高估等问题,DDPG实际运行的效果并不好。TwinDelayedDeep
Deterministic Policy Gradient (TD3) 可以大幅提升算法的表现,把策略网络和价值网络训练得更好。只是改进训练用的算法,并不改变神经网络的结构。
高估问题的解决方案——目标网络:
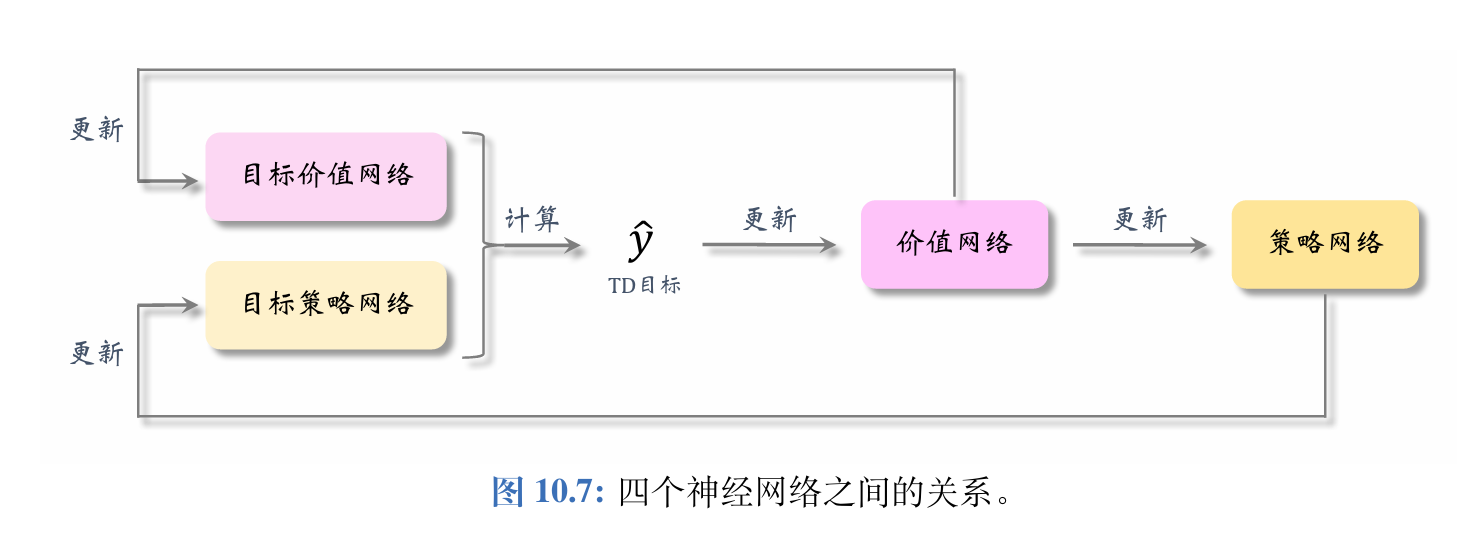
使用目标网络(Target Networks) 计算 TD 目标 y ^ j \widehat{y}_{j} y j,训练中需要两个目标网络:
q ( s , a ; w − ) 和 μ ( s ; θ − ) . q(s,\boldsymbol{a};\boldsymbol{w}^{-})\quad\text{和}\quad\boldsymbol{\mu}(s;\boldsymbol{\theta}^{-}). q(s,a;w−)和μ(s;θ−).
它们与价值网络、策略网络的结构完全相同,但是参数不同。
高估问题更好的解决方案——截断双Q学习(ClippedDoubleQ-Learning):
这种方法使用两个价值网络和一个策略网络:
q ( s , a ; w 1 ) , q ( s , a ; w 2 ) , μ ( s ; θ ) q(s,\boldsymbol{a};\boldsymbol{w}_1),\quad q(s,\boldsymbol{a};\boldsymbol{w}_2),\quad\boldsymbol{\mu}(s;\boldsymbol{\theta}) q(s,a;w1),q(s,a;w2),μ(s;θ)
三个神经网络各对应一个目标网络:
q ( s , a ; w 1 − ) , q ( s , a ; w 2 − ) , μ ( s ; θ − ) . q(s,\boldsymbol{a};\boldsymbol{w}_1^-),\quad q(s,\boldsymbol{a};\boldsymbol{w}_2^-),\quad\boldsymbol{\mu}(s;\boldsymbol{\theta}^-). q(s,a;w1−),q(s,a;w2−),μ(s;θ−).
1、离散控制问题的动作空间 A \mathcal A A是个有限的离散集合,连续控制问题的动作空间 A \mathcal A A是个连续集合,如果想将DQN等离散控制方法应用到连续控制问题上,可以对连续动作空间做离散化,但这只适用于自由度较低的问题。
2、可以用确定性策略网络 a = μ ( s ; θ ) a=\boldsymbol{\mu}(s;\boldsymbol{\theta}) a=μ(s;θ)做连续控制,网络的输人是状态 s s s,输出是动作 a a a,其中 a a a是向量,大小等于问题的自由度。
3、确定性策略梯度(DPG)借助价值网络 q ( s , a ; w ) q(s,\boldsymbol{a};\boldsymbol{w}) q(s,a;w)训练确定性策略网络,DPG属于异策略,用行为策略收集经验,做经验回放更新策略网络和价值网络。
4、DPG 与DQN有很多相似之处,而且它们的训练都存在高估等问题。TD3 使用三种技巧改进DPG:截断双Q学习,往动作中加噪声,以及降低更新策略网络和目标网络的频率。
5、可以用随机高斯策略做连续控制,用两个神经网络分别近似高斯分布的均值和方差对数,并用策略梯度更新两个神经网络的参数。
八、对状态的不完全观测
1、在强化学习的很多应用中,智能体无法完整观测到环境当前的状态 s t s_t st,可以把观测记作 o t o_t ot,以区别于完整的状态。仅仅基于当前观测状态 o t o_t ot做决策,效果会不理想。
2、一种合理的解决方案是记忆过去的状态,基于历史上全部的观测 o 1 , ⋯ , o t o_1,\cdots, o_t o1,⋯,ot做决策。常用循环神经网络(RNN)作为策略函数,做出的决策依赖于历史上全部的观测。
: Auto White Balance Gain Control (AWB) 自动白平衡)















)

)
