1. 多项式环(Polynomial Rings)
设 f∈Z[x]f \in \mathbb{Z}[x]f∈Z[x] 是首一多项式(最高次项系数为1)
则环 R=Z[x]/(f)R = \mathbb{Z}[x]/(f)R=Z[x]/(f)
元素为:所有次数 <deg(f)< \deg(f)<deg(f) 的多项式。
运算规则:
- 加法:逐系数模整数加法。
- 乘法:计算多项式乘积后模 f(x)f(x)f(x) 取余(余式次数 <deg(f)< \deg(f)<deg(f))。
多项式的向量表示:
多项式 a(x)=∑i=0n−1aixia(x) = \sum\limits_{i=0}^{n-1} a_i x^ia(x)=i=0∑n−1aixi 对应系数向量 a=(a0,a1,…,an−1)∈Zn\boldsymbol{a} = (a_0, a_1, \dots, a_{n-1}) \in \mathbb{Z}^na=(a0,a1,…,an−1)∈Zn。
例如:
R=Z[x]/(x4+2x2−11x+1)R = \mathbb{Z}[x]/(x^4 + 2x^2 -11x +1)R=Z[x]/(x4+2x2−11x+1) 中,
a(x)=23+11x2+7x3↔(23,0,11,7)a(x) = 23 + 11x^2 + 7x^3 \leftrightarrow (23, 0, 11, 7)a(x)=23+11x2+7x3↔(23,0,11,7).
2. 理想格(Ideal Lattices)
理想:
全称:理想子环
定义:(R,+,.)(R,+,.)(R,+,.)是环,III是RRR的非空子集。如果(I,+,.)(I,+,.)(I,+,.)满足以下条件:
- 加法子群:(I,+)(I,+)(I,+)是(R,+)(R,+)(R,+)的子群
- 乘法吸收律:∀r∈R,∀a∈I⇒ra∈I(ar∈I)\forall r\in R,\forall a \in I\Rightarrow ra\in I(ar\in I)∀r∈R,∀a∈I⇒ra∈I(ar∈I)
则称III是RRR的左(右)理想。
理想的判断:
(R,+,.)是环,I是R的左(右)理想,
∀a,b∈I,∀r∈R\forall a,b \in I ,\forall r \in R∀a,b∈I,∀r∈R当且仅当,III满足以下条件:
- 加法子群:(I,+)(I,+)(I,+)是(R,+)(R,+)(R,+)的子群(加法封闭性:a+b∈Ia+b \in Ia+b∈I加法逆元:−a∈I-a \in I−a∈I)
- 乘法吸收律:ra∈I(ar∈I)ra \in I(ar \in I)ra∈I(ar∈I)

理想三巨头:



主理想:由单个多项式生成 ⟨a(x)⟩={a(x)r(x)modf∣r∈R}\langle a(x) \rangle = \{ a(x) r(x) \mod f \mid r \in R \}⟨a(x)⟩={a(x)r(x)modf∣r∈R}。 ( 环 R=Z[x]/(f)R = \mathbb{Z}[x]/(f)R=Z[x]/(f) )
理想格:
理想 III 中所有多项式系数向量构成的整数格 L(I)⊂RnL(I) \subset \mathbb{R}^nL(I)⊂Rn。(理想本身就满足群的性质)
本篇仅考虑 f(x)=xn−1f(x) = x^n - 1f(x)=xn−1(循环格)或 f(x)=xn+1f(x) = x^n + 1f(x)=xn+1(反循环格)。
3. 循环格与反循环格(结构化的格)
(1)循环格
循环格最早在2002年被Micciancio研究
定义:
设 L⊆ZnL \subseteq \mathbb{Z}^nL⊆Zn 是一个格。若对任意向量 v=(v0,v1,…,vn−1)∈L\boldsymbol{v} = (v_0, v_1, \dots, v_{n-1}) \in Lv=(v0,v1,…,vn−1)∈L,其左循环移位 (vn−1,v0,v1,…,vn−2)∈L(v_{n-1}, v_0, v_1, \dots, v_{n-2}) \in L(vn−1,v0,v1,…,vn−2)∈L,则 LLL 称为循环格。
定理:
R=Z[x]/(xn−1)R=\mathbb{Z}[x]/(x^n-1)R=Z[x]/(xn−1),则其每一个理想格都是循环格。
ps理想与格关系:每个理想都对应一个格(理想定义天然包含离散子群的条件)
主理想中的多项式通过系数提取转化为向量,这些向量的全体构成一个格。
对 R=Z[x]/(xn−1)R = \mathbb{Z}[x]/(x^n - 1)R=Z[x]/(xn−1) 的主理想III= ⟨a(x)⟩\langle a(x) \rangle⟨a(x)⟩,I={a(x)⋅r(x)mod(xn−1)∣r(x)∈R}I = \left\{ a(x) \cdot r(x) \bmod (x^n - 1) \mid r(x) \in R \right\}I={a(x)⋅r(x)mod(xn−1)∣r(x)∈R}
则其对应的格 ( L(I)L(I)L(I) ) 定义为: L(I)={系数向量∣p(x)∈I}={s∈Zn∣s=Ar,r∈Zn}L(I) = \{\text{系数向量} \mid p(x) \in I\} = \{\boldsymbol{s} \in \mathbb{Z}^n \mid \boldsymbol{s} = \boldsymbol{A}\boldsymbol{r},\ \boldsymbol{r} \in \mathbb{Z}^n\} L(I)={系数向量∣p(x)∈I}={s∈Zn∣s=Ar, r∈Zn} 其中 (A\boldsymbol{A}A) 是循环矩阵。
注:(乘积 s(x)=a(x)⋅r(x)mod(xn−1)s(x) = a(x) \cdot r(x) \bmod (x^n - 1)s(x)=a(x)⋅r(x)mod(xn−1) 的系数向量 s\boldsymbol{s}s 由循环卷积给出: sk=∑i+j≡k(modn)airjs_k = \sum\limits_{\substack{i+j \equiv k \pmod{n}}} a_i r_jsk=i+j≡k(modn)∑airj 这等价于矩阵乘法 s=Ar\boldsymbol{s} = \boldsymbol{A}\boldsymbol{r}s=Ar。)
关键理解
设 a(x)=a0+a1x+⋯+an−1xn−1a(x) = a_0 + a_1 x + \cdots + a_{n-1} x^{n-1}a(x)=a0+a1x+⋯+an−1xn−1,其系数向量为 a=(a0,a1,…,an−1)⊤\boldsymbol{a} = (a_0, a_1, \ldots, a_{n-1})^\topa=(a0,a1,…,an−1)⊤。
理想 III 是z−\mathbb{z}-z−模的生成元是集合 {a(x),xa(x),x2a(x),…,xn−1a(x)}\{ a(x), x a(x), x^2 a(x), \ldots, x^{n-1} a(x) \}{a(x),xa(x),x2a(x),…,xn−1a(x)}。
因为:
将 r(x)r(x)r(x) 代入 III 中元素的表达式,得: a(x)⋅r(x)=a(x)⋅(r0+r1x+⋯+rn−1xn−1)=r0⋅a(x)+r1⋅(xa(x))+⋯+rn−1⋅(xn−1a(x))a(x) \cdot r(x) = a(x) \cdot \left( r_0 + r_1 x + \cdots + r_{n-1} x^{n-1} \right) = r_0 \cdot a(x) + r_1 \cdot \left( x a(x) \right) + \cdots + r_{n-1} \cdot \left( x^{n-1} a(x) \right) a(x)⋅r(x)=a(x)⋅(r0+r1x+⋯+rn−1xn−1)=r0⋅a(x)+r1⋅(xa(x))+⋯+rn−1⋅(xn−1a(x)) 这说明:III 中任意元素都是 {a(x),xa(x),…,xn−1a(x)}\{ a(x), x a(x), \ldots, x^{n-1} a(x) \}{a(x),xa(x),…,xn−1a(x)} 的 整数线性组合(系数 ri∈Zr_i \in \mathbb{Z}ri∈Z)。
即集合 {a(x),xa(x),x2a(x),…,xn−1a(x)}\{ a(x), xa(x), x^2a(x), \dots, x^{n-1}a(x) \}{a(x),xa(x),x2a(x),…,xn−1a(x)} 的系数向量张成格 L(I)L(I)L(I),其矩阵形式为循环矩阵.
A=circ(a)=[a0an−1⋯a1a1a0⋯a2⋮⋮⋱⋮an−1an−2⋯a0]\boldsymbol{A} = \text{circ}(\boldsymbol{a}) = \begin{bmatrix} a_0 & a_{n-1} & \cdots & a_1 \\ a_1 & a_0 & \cdots & a_2 \\ \vdots & \vdots & \ddots & \vdots \\ a_{n-1} & a_{n-2} & \cdots & a_0 \end{bmatrix} A=circ(a)=a0a1⋮an−1an−1a0⋮an−2⋯⋯⋱⋯a1a2⋮a0
A可逆条件:gcd(a(x),xn−1)=1\gcd(a(x), x^n - 1) = 1gcd(a(x),xn−1)=1(在 Q\mathbb{Q}Q 上)。
记作:A=circ(a)\boldsymbol{A} = \text{circ}(\boldsymbol{a})A=circ(a)
(2) 反循环格
定义:
设 L⊆ZnL \subseteq \mathbb{Z}^nL⊆Zn 是一个格。若对任意向量 v=(v0,v1,…,vn−1)∈L\boldsymbol{v} = (v_0, v_1, \dots, v_{n-1}) \in Lv=(v0,v1,…,vn−1)∈L,其反循环移位 (−vn−1,v0,v1,…,vn−2)∈L(-v_{n-1}, v_0, v_1, \dots, v_{n-2}) \in L(−vn−1,v0,v1,…,vn−2)∈L,则 LLL 称为反循环格。
定理:
设 R=Z[x]/(xn+1)R = \mathbb{Z}[x]/(x^n + 1)R=Z[x]/(xn+1),则其每一个理想格都是反循环格。
ps 理想与格关系:每个理想都对应一个格(理想定义天然包含离散子群的条件)。
主理想中的多项式通过系数提取转化为向量,这些向量的全体构成一个格。
主理想对应的格
对 R=Z[x]/(xn+1)R = \mathbb{Z}[x]/(x^n + 1)R=Z[x]/(xn+1) 的主理想 I=⟨a(x)⟩I = \langle a(x) \rangleI=⟨a(x)⟩,
I={a(x)⋅r(x)mod(xn+1)∣r(x)∈R}I = \left\{ a(x) \cdot r(x) \bmod (x^n + 1) \mid r(x) \in R \right\}I={a(x)⋅r(x)mod(xn+1)∣r(x)∈R}
则其对应的格 L(I)L(I)L(I) 定义为:
L(I)={系数向量∣p(x)∈I}={s∈Zn∣s=Br,r∈Zn}L(I) = \{\text{系数向量} \mid p(x) \in I\} = \{\boldsymbol{s} \in \mathbb{Z}^n \mid \boldsymbol{s} = \boldsymbol{B}\boldsymbol{r},\ \boldsymbol{r} \in \mathbb{Z}^n\}L(I)={系数向量∣p(x)∈I}={s∈Zn∣s=Br, r∈Zn}
其中 B\boldsymbol{B}B 是反循环矩阵。
注:(乘积 s(x)=a(x)⋅r(x)mod(xn+1)s(x) = a(x) \cdot r(x) \bmod (x^n + 1)s(x)=a(x)⋅r(x)mod(xn+1) 的系数向量 s\boldsymbol{s}s 由反循环卷积给出:
sk=∑i+j≡k(modn)i+j<nairj−∑i+j≡k+n(modn)i+j≥nairjs_k = \sum_{\substack{i + j \equiv k \pmod{n} \\ i + j < n}} a_i r_j - \sum_{\substack{i + j \equiv k + n \pmod{n} \\ i + j \geq n}} a_i r_jsk=∑i+j≡k(modn)i+j<nairj−∑i+j≡k+n(modn)i+j≥nairj
这等价于矩阵乘法 s=Br\boldsymbol{s} = \boldsymbol{B}\boldsymbol{r}s=Br。
关键理解
设 a(x)=a0+a1x+⋯+an−1xn−1a(x) = a_0 + a_1 x + \cdots + a_{n-1} x^{n-1}a(x)=a0+a1x+⋯+an−1xn−1,其系数向量为 a=(a0,a1,…,an−1)⊤\boldsymbol{a} = (a_0, a_1, \ldots, a_{n-1})^\topa=(a0,a1,…,an−1)⊤。
理想 III 作为 Z\mathbb{Z}Z-模的生成元是集合 {a(x),xa(x),x2a(x),…,xn−1a(x)}\{ a(x), x a(x), x^2 a(x), \ldots, x^{n-1} a(x) \}{a(x),xa(x),x2a(x),…,xn−1a(x)}。
因为:
将 r(x)r(x)r(x) 代入 III 中元素的表达式,得:
a(x)⋅r(x)=a(x)⋅(r0+r1x+⋯+rn−1xn−1)=r0⋅a(x)+r1⋅(xa(x))+⋯+rn−1⋅(xn−1a(x))a(x) \cdot r(x) = a(x) \cdot \left( r_0 + r_1 x + \cdots + r_{n-1} x^{n-1} \right) = r_0 \cdot a(x) + r_1 \cdot \left( x a(x) \right) + \cdots + r_{n-1} \cdot \left( x^{n-1} a(x) \right)a(x)⋅r(x)=a(x)⋅(r0+r1x+⋯+rn−1xn−1)=r0⋅a(x)+r1⋅(xa(x))+⋯+rn−1⋅(xn−1a(x))
这说明:III 中任意元素都是 {a(x),xa(x),…,xn−1a(x)}\{ a(x), x a(x), \ldots, x^{n-1} a(x) \}{a(x),xa(x),…,xn−1a(x)} 的整数线性组合(系数 ri∈Zr_i \in \mathbb{Z}ri∈Z)。
即集合 {a(x),xa(x),x2a(x),…,xn−1a(x)}\{ a(x), x a(x), x^2 a(x), \dots, x^{n-1} a(x) \}{a(x),xa(x),x2a(x),…,xn−1a(x)} 的系数向量张成格 L(I)L(I)L(I),其矩阵形式为反循环矩阵:
B=circ‾(a)=[a0−an−1−an−2⋯−a1a1a0−an−1⋯−a2a2a1a0⋯−a3⋮⋮⋮⋱⋮an−1an−2an−3⋯a0]\boldsymbol{B} = \overline{\text{circ}}(\boldsymbol{a}) = \begin{bmatrix} a_0 & -a_{n-1} & -a_{n-2} & \cdots & -a_1 \\ a_1 & a_0 & -a_{n-1} & \cdots & -a_2 \\ a_2 & a_1 & a_0 & \cdots & -a_3 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n-1} & a_{n-2} & a_{n-3} & \cdots & a_0 \end{bmatrix}B=circ(a)=a0a1a2⋮an−1−an−1a0a1⋮an−2−an−2−an−1a0⋮an−3⋯⋯⋯⋱⋯−a1−a2−a3⋮a0
B\boldsymbol{B}B 可逆条件:gcd(a(x),xn+1)=1\gcd(a(x), x^n + 1) = 1gcd(a(x),xn+1)=1(在 Q\mathbb{Q}Q 上)。
记作B=circ‾(a)\boldsymbol{B} = \overline{\text{circ}}(\boldsymbol{a})B=circ(a)
密码学意义对比
| 特性 | 循环格 | 反循环格 |
|---|---|---|
| 多项式环 | Z[x]/(xn−1)\mathbb{Z}[x]/(x^n - 1)Z[x]/(xn−1) | Z[x]/(xn+1)\mathbb{Z}[x]/(x^n + 1)Z[x]/(xn+1) |
| 安全强度 | 较低(xn−1x^n-1xn−1 可因式分解) | 较高(xn+1x^n+1xn+1 不可约) |
| 移位操作 | (vn−1,v0,…,vn−2)(v_{n-1}, v_0, \dots, v_{n-2})(vn−1,v0,…,vn−2) | (−vn−1,v0,…,vn−2)(-v_{n-1}, v_0, \dots, v_{n-2})(−vn−1,v0,…,vn−2) |
| 应用场景 | 早期方案(Micciancio 2002) | 后量子密码标准(Kyber, Dilithium) |
注:反循环格在现代密码学中更常用,因 xn+1x^n + 1xn+1 在 n=2wn=2^wn=2w 时不可约,提供更强的安全性保证。
4. Ring-SIS
2006年由Micciancio和Rosen提出
Ring-SIS(n,ℓ,q,B)(n,\ell,q,B)(n,ℓ,q,B)安全参数 nnn(通常为2的幂),模数 qqq,目标向量数量 ℓ\ellℓ,范数界 BBB
定义
给定a1,…,aℓ∈Rq=Zq[x]/(xn+1)a_1, \dots, a_\ell \in R_q = \mathbb{Z}_q[x]/(x^n + 1)a1,…,aℓ∈Rq=Zq[x]/(xn+1)。找到非零 z1,…,zℓ∈Rqz_1, \dots, z_\ell \in R_qz1,…,zℓ∈Rq,使得(多项式卷积相乘)
∑i=1ℓaizi=0(modq),∥zi∥∞≤B.\sum_{i=1}^\ell a_i z_i = 0 \pmod{q}, \quad \|z_i\|_\infty \leq B. i=1∑ℓaizi=0(modq),∥zi∥∞≤B.
等价向量形式:构造分块反循环矩阵 m=(ℓ×n)m=(\ell \times n)m=(ℓ×n)
A=[circ‾(a1)∣⋯∣circ‾(aℓ)]n×m\boldsymbol{A} = [\overline{\text{circ}}(\boldsymbol{a}_1) \mid \cdots \mid \overline{\text{circ}}(\boldsymbol{a}_\ell)]_{n\times m}A=[circ(a1)∣⋯∣circ(aℓ)]n×m,求非零短向量 z∈[−B,B]m\boldsymbol{z}\in[-B,B]^mz∈[−B,B]m 使 Az≡0(modq)\boldsymbol{A}\boldsymbol{z} \equiv 0 \pmod{q}Az≡0(modq)。
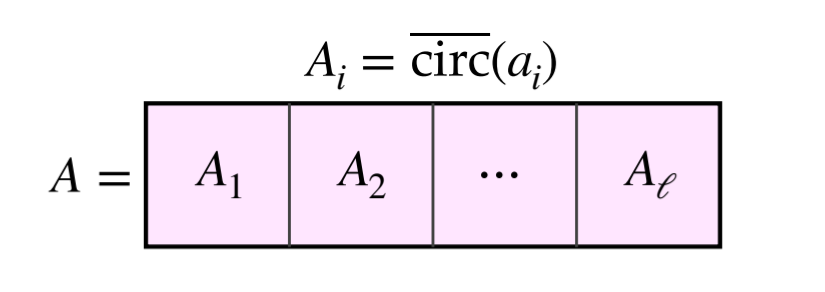
Lyubashevsky和Micciancio证明,求解平均情况下的环-SIS(Ring-SIS\text{Ring-SIS}Ring-SIS)问题,至少与求解最坏情况下反循环格的 γ\gammaγ-最短向量问题(SVPγ\text{SVP}_\gammaSVPγ)一样困难。
应用:

5. Ring-LWE
2010年由Lyubashevsky、Peikert和Rosen提出
Ring-LWE(n,k,q,B)(n, k, q, B)(n,k,q,B)安全参数:nnn(通常为2的幂,即n=2wn=2^wn=2w),实例数量kkk,模数qqq,误差界BBB(满足B≪q/2B \ll q/2B≪q/2)
定义
给定a1,…,ak∈Rq=Zq[x]/(xn+1)a_1, \dots, a_k \in R_q = \mathbb{Z}_q[x]/(x^n + 1)a1,…,ak∈Rq=Zq[x]/(xn+1)和b1,…,bk∈Rqb_1, \dots, b_k \in R_qb1,…,bk∈Rq,其中bi=ais+eib_i = a_i s + e_ibi=ais+ei(s,eis, e_is,ei为“短多项式”,即系数均在[−B,B][-B, B][−B,B]中)。找到秘密多项式s∈Rqs \in R_qs∈Rq,使得对所有i=1,…,ki=1,\dots,ki=1,…,k,均满足:
bi≡ais+ei(modq),∥s∥∞≤Bs,∥ei∥∞≤Be.b_i \equiv a_i s + e_i \pmod{q}, \quad \|s\|_\infty \leq B_s, \quad \|e_i\|_\infty \leq B_e.bi≡ais+ei(modq),∥s∥∞≤Bs,∥ei∥∞≤Be.
等价向量形式
构造分块反循环矩阵:
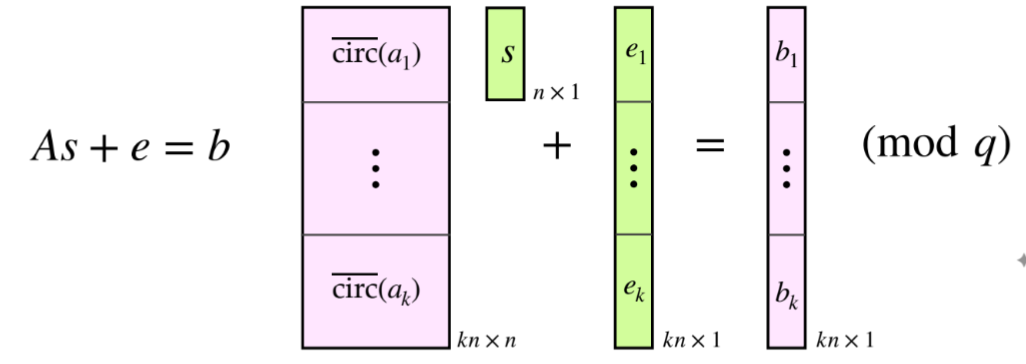
A=[circ‾(a1)circ‾(a2)⋮circ‾(ak)]kn×n\boldsymbol{A} = \begin{bmatrix} \overline{\text{circ}}(\boldsymbol{a}_1) \\ \overline{\text{circ}}(\boldsymbol{a}_2) \\ \vdots \\ \overline{\text{circ}}(\boldsymbol{a}_k) \end{bmatrix}_{kn \times n}A=circ(a1)circ(a2)⋮circ(ak)kn×n
其中circ‾(ai)\overline{\text{circ}}(\boldsymbol{a}_i)circ(ai)是ai\boldsymbol{a}_iai的反循环矩阵(n×nn \times nn×n)。则问题等价于求解nnn维向量s\boldsymbol{s}s和knknkn维误差向量e∈[−B,B]kn\boldsymbol{e} \in [-B, B]^{kn}e∈[−B,B]kn,使得:
As+e≡b(modq)\boldsymbol{A} \boldsymbol{s} + \boldsymbol{e} \equiv \boldsymbol{b} \pmod{q}As+e≡b(modq)
(b\boldsymbol{b}b是b1,…,bkb_1, \dots, b_kb1,…,bk的系数向量拼接而成的knknkn维向量)。
安全归约
Lyubashevsky、Peikert和Rosen证明:求解平均情况下的Ring-LWE问题,至少与量子算法求解最坏情况下反循环格的γ\gammaγ-最短整数向量问题(SIVPγ\text{SIVP}_\gammaSIVPγ)一样困难。
目前尚未发现利用矩阵A\boldsymbol{A}A的结构(反循环性)加速求解的攻击,其安全性与一般LWE相当,但效率更高。
应用:

参考资料:
【理想】理想就是一种子环,它具有乘法吸收律_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1rm4y1r7dV/?spm_id_from=333.1387.top_right_bar_window_history.content.click
https://cryptography101.ca/lattice-based-cryptography/








![[硬件电路-20]:模拟信号处理运算与数字信号处理运算的相同点与不同点](http://pic.xiahunao.cn/[硬件电路-20]:模拟信号处理运算与数字信号处理运算的相同点与不同点)



)
![[智能算法]MOEA/D算法的Python实现](http://pic.xiahunao.cn/[智能算法]MOEA/D算法的Python实现)


)


