软活硬整，纳什又把RL翻出来讲了一遍，我以为是温故而知新，原来是在卖书。

不过温故而知新还是没啥毛病的。

PS：今天装Notepad++时看到的，我还以为现在连用个Notepad++都要给天线宝宝们捐款了。

---

---

PART 1

video: https://www.bilibili.com/video/BV1i8TQzuEKs
code: https://github.com/chunhuizhang/modern_ai_for_beginners/blob/main/books_reading_notes/RL/%E5%BC%BA%E5%8C%96%E5%AD%A6%E4%B9%A0%E7%9A%84%E6%95%B0%E5%AD%A6%E5%8E%9F%E7%90%86.ipynb

1 overview

https://github.com/MathFoundationRL/Book-Mathematical-Foundation-of-Reinforcement-Learning

• Chap1：基本概念
• Chap2-Chap8：value-based methods
  • 先估计值再得到最优策略；
    • 估计一个策略的 action value，就叫 policy evaluation，在此基础上选择更好的策略，再去进行采样然后不断地迭代循环；
  • Chap2-3：Bellman equation
  • Chap4：VI（Value Iteration）& PI（Policy Iteration）
  • Chap5：MC (monte-carlo 方法，model-free)
  • Chap7：TD
• Chap9-10：policy-based methods，直接优化关于策略参数 ${\pi }_{\theta }(a|s)$ 的目标函数（通过优化这个目标函数直接得到最优策略）
  • Chap9：PG（policy gradient）
    • https://www.bilibili.com/video/BV1sd4y167NS
    • 策略梯度定理
      • simple code：
        • https://www.datacamp.com/tutorial/policy-gradient-theorem
  • Chap10：Actor-Critic (A2C)，融合了基于策略和基于价值的两类方法
    • Actor：策略更新
    • Critic：价值更新
• 这本书跟神经网络或者DRL是兼容的
  • 比如这里就有：
    • 【强化学习的数学原理】课程：从零开始到透彻理解（完结）：https://www.bilibili.com/video/BV1sd4y167NS
  • 用函数（而非表格）表示时，$v_w(s),{\pi }_{\theta }(a|s)$ 均可以为神经网络 parameterized by $w,\theta$ respectively

---

2 highlights

从现代应用的视角，rlhf (ppo), rl4llm (ppo-variants)

• policy gradient 之于 RL，犹如 attention 之于 transformer
  • 很基础很本质，很核心
• 像一个分水岭，
  • 往后就是一系列应用（rl4llm，policy-gradient based 方法是 most popular 的方法）
  • 往前就是 RL 基础概念基本原理的准备；

3 Core concepts

3.1 $R_T$ v.s. $G_t$

$$\begin{array}{rl}& J(\theta )=E[G_t]=E[G_0]\\ & J(\theta )={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}[G_0]={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[\sum _{t=0}^{T-1}{\gamma }^t{R}_{t+1}\right]\end{array}$$

• 奖励（reward，$R_t$）与回报（return，$G_t$）
  • $R_t$：智能体在特定时间点 $t$ 完成某个动作后立即给予的反馈。
    • $(s_t,a_t,r_{t+1})$
  • $G_t$：回报是衡量从某一时刻开始，直到“一局游戏”结束，智能体能够获得的“总奖励”是多少。因为未来的奖励可能不如眼前的奖励那么确定或有价值，我们通常会给未来的奖励打个折扣。
    • discounted cumulative future reward
    • $G_t={\sum }_{k=t+1}^T{\gamma }^{k-t}{r}_k$
• 智能体的目标不是最大化瞬时奖励 $R_t$，而是最大化累积奖励。

3.2 value/advantage function

• 状态价值函数：$V(s)$
  • $V_{\pi }(s)=E_{\pi }[G_t|S_t=s]$
• 动作值函数: $Q(s,a)$
  • $Q_{\pi }(s,a)=E_{\pi }[G_t|S_t=s,A_t=a]$
  • $G_t$ 是对 $Q^{{\pi }_{\theta }}(s_t,a_t)$ 的无偏采样。
• 优势函数 (Advantage Function, $A(s,a)$)
  • $A_{\pi }(s,a)=Q_{\pi }(s,a)-V_{\pi }(s)$

3.3 Bellman equation

贝尔曼期望方程 (Bellman Expectation Equations)

$$\begin{array}{rl}{V}^{\pi }(s)& =\sum _{a\in A}\pi (a|s)\sum _{s^{\prime },r}P(s^{\prime },r|s,a)[r+\gamma V^{\pi }(s^{\prime })]\\ Q^{\pi }(s,a)& =\sum _{s^{\prime },r}P(s^{\prime },r|s,a)[r+\gamma \sum _{a^{\prime }\in A}\pi (a^{\prime }|s^{\prime })Q^{\pi }(s^{\prime },a^{\prime })]\\ V(s)& =\sum _{a\in A}\pi (a|s)Q(s,a)\end{array}$$
或者，更简洁地，如果 $V^{\pi }(s^{\prime })$ 已知： $Q^{\pi }(s,a)={\sum }_{s^{\prime },r}P(s^{\prime },r|s,a)[r+\gamma V^{\pi }(s^{\prime })]$.

它为特定策略 π 下的状态价值函数 $V_{\pi }$ (或动作价值函数 $Q_{\pi }$) 提供了一个自洽的递归定义：当前状态的价值等于遵循该策略所能获得的即时奖励，加上所有可能的下一状态的折扣价值的期望。其关键作用是作为评估一个给定策略好坏的数学基石：通过求解该方程，可以精确计算出在该策略指导下，从每个状态出发能获得的长期期望回报，从而量化策略的性能，并成为策略迭代等算法中“策略评估”步骤的理论核心。

---

贝尔曼最优方程 (Bellman Optimality Equations):

$$\begin{array}{r}V(s)=\underset{a}{\max }\sum _{s^{\prime },r}P(s^{\prime },r|s,a)[r+\gamma V^{(}{s}^{\prime })]\\ Q(s,a)=\sum _{s^{\prime },r}P(s^{\prime },r|s,a)[r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })]\end{array}$$ 且 $V(s)={\max }_{a}Q(s,a)$

---

想象你是一个寻宝者，在一张藏宝图（代表环境）上寻找价值最高的宝藏。地图上有很多地点（状态），你可以从一个地点移动到另一个地点（动作），每次移动可能会得到一些小奖励或付出一些代价，最终目标是找到一条路径，使得总奖励最大。

• 值迭代 (Value Iteration, VI)：先搞清楚每个地点有多“值钱”，再决定怎么走。
  • 迭代的是价值函数
• 策略迭代 (Policy Iteration, PI)：先定个初步的行走计划，然后评估这个计划好不好，再改进计划，如此循环。
  • 迭代的是策略 (虽然中间会计算价值函数)

值迭代算法直接将贝尔曼最优方程转化为一个迭代更新规则来寻找最优状态值函数 $V^{\ast }(s)$

• $V_{k+1}(s)\leftarrow {\max }_a{\sum }_{s^{\prime },r}P(s^{\prime },r|s,a)[r+\gamma V_k(s^{\prime })]$

一旦得到 收敛后的值函数就是最优状态值函数 $V^{\ast }(s)$，就可以从中提取出最优策略 ${\pi }^{\ast }(s)=\arg {\max }_a{\sum }_{s^{\prime },r}P(s^{\prime },r|s,a)[r+\gamma V^{\ast }(s^{\prime })]$

3.4 MC v.s. TD

当任务是分幕式 (episodic) 的，即有明确的开始和结束（比如一盘棋，一次走迷宫）。

• 智能体需要完整地采样一条轨迹 (trajectory) $\tau =(S_0,A_0,R_1,S_1,A_1,R_2,...,S_{T-1},A_{T-1},R_T,S_T)$，其中 T 是终止状态的时间步。
• 对于这条轨迹中的每一步 t，回报 $G_t$ 计算如下： $G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...+{\gamma }^{T-t-1}{R}_T={\sum }_{k=0}^{T-t-1}{\gamma }^k{R}_{t+k+1}$ 这里的 $R_{t+1}$ 是在状态 $S_t$ 执行动作 $A_t$ 后得到的即时奖励。$G_t$ 是从 $S_t$ 状态之后，未来所有步骤能获得的折扣奖励总和。
  • 计算的局限性，只要没抵达目标，就无法确定收益 $G_t$ 的值；

如果任务不是分幕式的 (continuing tasks)，或者我们不想等到整个 episode 结束才计算回报（比如在时序差分学习 TD learning 中）

• 回报 $G_t$ 通常会用值函数来估计。 例如，在一步 TD 学习中，回报 $G_t$ (也称为 TD 目标) 可以估计为： $G_t\approx R_{t+1}+\gamma V(S_{t+1})$
  • 这里 $V(S_{t+1})$ 是对状态 $S_{t+1}$ 未来价值的一个估计。这就像是说：“我先拿上眼前的奖励 $R_{t+1}$，然后估计一下我到达的新状态 $S_{t+1}$ 大概还能带来多少未来的折扣奖励 $\gamma V(S_{t+1})$。”

---

4 Policy Gradient

$${\theta }_{t+1}\leftarrow {\theta }_t+\alpha {\nabla }_{\theta }J({\theta }_t)$$

• 梯度方向，指向函数值增加最快的方向（梯度上升 => 最大化）：在函数定义域内的任何一点，该点的梯度向量所指的方向是函数值上升最陡峭的方向
  • $y=-x^2,y^{\prime }=-2x$
    • $x\leftarrow x+0.01y^{\prime }$
      • $x=1,x=1-0.02$，向左移动（向 0 点靠近）
      • $x=-1,x=-1+0.02$，向右移动（向 0 点靠近）
  • $\theta =\theta +\alpha \ast {\nabla }_{\theta }f(\theta )$
  • 梯度下降（gradient descent），沿着梯度的反方向，最小化目标；
    • $\theta =\theta -\alpha \ast {\nabla }_{\theta }f(\theta )$
• ${\nabla }_{\theta }\log {\pi }_{\theta }(A_t|S_t)$ 本身的方向就是使得 ${\pi }_{\theta }(A_t|S_t)$ 增加的方向。
  • ${\nabla }_{\theta }\log {\pi }_{\theta }=\frac{{\nabla }_{\theta }{\pi }_{\theta }}{{\pi }_{\theta }}$, ${\pi }_{\theta }$ 概率密度函数一定是 $>0$ 的；
  • ${\nabla }_{\theta }\log {\pi }_{\theta }$ 方向与 ${\nabla }_{\theta }{\pi }_{\theta }$ 方向相同，这个梯度方向显然就是 ${\pi }_{\theta }$ 取值增加的方向
    • 提升 ${\pi }_{\theta }(a|s)$ 的概率；

$$J(\theta )=E[G_t]=E_{\tau \sim {\pi }_{\theta }}[G_0]$$

• https://en.wikipedia.org/wiki/Policy_gradient_method
  • log-derivate trick：方便整理成策略的期望形式
    • $f^{\prime }=f\nabla \log f=f\left(\frac{f^{\prime }}{f}\right)$
    • $\nabla {\pi }_{\theta }={\pi }_{\theta }{\nabla }_{\theta }\log {\pi }_{\theta }$

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\begin{array}{c}s\sim d^{{\pi }_{\theta }}a\sim {\pi }_{\theta }(\cdot |s)\end{array}}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(a|s)\cdot R(s,a)\right]$$

• $R(s,a)$ （也可以理解为对当前状态 $s$ 下选择动作 $a$ 的奖励分配）的常见形式及其期望下标：
  • $G_t$ (累积回报 Total Return): 这是 REINFORCE 算法中使用的形式。${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[{\sum }_{t=0}^{T-1}{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)G_t\right]$
    • $G_t={\sum }_{k=t+1}^T{\gamma }^{k-t}{r}_k$
    • 如果在状态 $s_t$ 执行动作 $a_t$ 后，最终得到的未来总回报 $G_t$ 比较高，那么我们就应该增加在 $s_t$ 选择 $a_t$ 的概率（通过增大 $\log {\pi }_{\theta }(a_t|s_t)$）。反之，如果 $G_t$ 比较低，就减小选择该动作的概率。
    • 无偏估计：$G_t$ 是对 $Q^{{\pi }_{\theta }}(s_t,a_t)$ 的无偏采样。
      • $Q^{\pi_\theta}(s_t, a_t) = \mathbb{E}{\pi\theta} [G_t | S_t=s_t, A_t=a_t] $
    • 高方差：$G_t$ 是通过（MC，monte carlo）采样一条完整的轨迹得到的（基于当前不完美的 ${\pi }_{\theta }(a_t|s_t)$ 得到的），其随机性很大，导致梯度的方差很高，学习过程不稳定且收敛慢。（因此替换为$Q^{{\pi }_{\theta }}(s,a)$）
  • $Q^{{\pi }_{\theta }}(s,a)$: ${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\begin{array}{c}s\sim d^{{\pi }_{\theta }}\\ a\sim {\pi }_{\theta }(\cdot |s)\end{array}}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(a|s)Q^{{\pi }_{\theta }}(s,a)\right]$
    • Q AC（Q actor critic）涉及两个模型： ${\pi }_{\theta }(a|s)$, $Q_w(s,a)$
    • Critic 负责评估在某个状态下执行某个动作有多好（$Q_w(s,a)$），Actor 则根据 Critic 的评估来调整自己的动作选择概率。如果 Critic 说某个动作好，Actor 就更倾向于选择它。
    • 减小方差：$Q_w(s,a)$ 通常是基于更多经验学习得到的，相比单次采样的 $G_t$，它更为平滑，从而可以减小梯度的方差。
  • $A^{{\pi }_{\theta }}(s,a)$ (优势函数 Advantage Function): ${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\begin{array}{c}s\sim d^{{\pi }_{\theta }}\\ a\sim {\pi }_{\theta }(\cdot |s)\end{array}}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(a|s)A^{{\pi }_{\theta }}(s,a)\right]$
    • A2C（Advantage Actor Critic），涉及两个模型 ${\pi }_{\theta }(a|s)$, $V_w(s)$
    • $A^{{\pi }_{\theta }}(s,a)=Q^{{\pi }_{\theta }}(s,a)-V_w(s)$
      • 一种非常常见且有效的方式是使用 TD error 作为优势函数的估计： 对于一个在时间步 $t$ 的转移 $(s_t,a_t,r_{t+1},s_{t+1})$
        • $Q^{{\pi }_{\theta }}(s_t,a_t)$ 可以用一步 TD 目标来估计 $r_{t+1}+\gamma V_w(s_{t+1})$
        • 优势函数的估计 ${\hat{A}}_t$ 就变成了：${\hat{A}}_t=(r_{t+1}+\gamma V_w(s_{t+1}))-V_w(s_t)$
      • Actor(${\pi }_{\theta }(a|s)$) 根据 ${\hat{A}}_t$ 来更新其参数 $\theta$。如果 ${\hat{A}}_t>0$，则增加 $\log {\pi }_{\theta }(a_t|s_t)$；反之则减少。
      • Critic($V_w(s)$)，学习去最小化 TD error，即让 $V(s_t)$ 尽可能接近 $r_{t+1}+\gamma V_w(s_{t+1})$

---

$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& \propto \sum _s{d}^{{\pi }_{\theta }}(s)\sum _a({\nabla }_{\theta }{\pi }_{\theta }(a|s))Q^{{\pi }_{\theta }}(s,a)\\ & \text{(An intermediate step in Policy Gradient theorem derivation)}\\ & \\ & \text{The log-derivative trick states: }{\nabla }_{x}f(x)=f(x){\nabla }_x\log f(x).\\ & \text{Applying this with }f(x)={\pi }_{\theta }(a|s)\text{ (the policy) and variable }\theta :\\ {\nabla }_{\theta }{\pi }_{\theta }(a|s)& ={\pi }_{\theta }(a|s){\nabla }_{\theta }\log {\pi }_{\theta }(a|s).\\ & \\ & \text{Substituting this identity back into the expression for }{\nabla }_{\theta }J(\theta ):\\ {\nabla }_{\theta }J(\theta )& \propto \sum _s{d}^{{\pi }_{\theta }}(s)\sum _a\left({\pi }_{\theta }(a|s){\nabla }_{\theta }\log {\pi }_{\theta }(a|s)\right)Q^{{\pi }_{\theta }}(s,a)\\ & =\sum _s{d}^{{\pi }_{\theta }}(s)\sum _a{\pi }_{\theta }(a|s)\left[{\nabla }_{\theta }\log {\pi }_{\theta }(a|s)Q^{{\pi }_{\theta }}(s,a)\right]\\ & ={\mathbb{E}}_{\begin{array}{c}s\sim d^{{\pi }_{\theta }}\\ a\sim {\pi }_{\theta }(\cdot |s)\end{array}}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(a|s)Q^{{\pi }_{\theta }}(s,a)\right]\end{array}$$

• $d^{{\pi }_{\theta }}(s)$: 在策略 ${\pi }_{\theta }$ 下的状态分布

4.1 ${\nabla }_{\theta }J(\theta )\approx {\sum }_{t=0}^{T-1}\underset{\text{方向}}{\underbrace{{\nabla }_{\theta }\log {\pi }_{\theta }(A_t|S_t)}}\underset{\text{幅度与符号}}{\underbrace{G_t}}$

$$\begin{array}{rl}& \theta \leftarrow \theta +\alpha \cdot {\nabla }_{\theta }J(\theta )\\ & \theta \leftarrow \theta +\alpha \cdot \left(\sum _{t=0}^{T-1}{\nabla }_{\theta }\log {\pi }_{\theta }(A_t|S_t)G_t\right)\end{array}$$

• 如果 $G_t$ 是正的且较大，说明从 $(S_t,A_t)$ 开始的后续表现很好，那么我们就希望增加在 $S_t$ 状态下选择 $A_t$ 动作的概率。
  • ${\pi }_{\theta }(A_t|S_t)\uparrow$
  • ${\nabla }_{\theta }\log {\pi }_{\theta }(A_t|S_t)\cdot G_t$ 与 ${\nabla }_{\theta }\log {\pi }_{\theta }(A_t|S_t)$ 方向相同
• 如果 $G_t$ 是负的或较小，说明后续表现不好，那么我们就希望减少在 $S_t$ 状态下选择 $A_t$ 动作的概率。
  • ${\pi }_{\theta }(A_t|S_t)\downarrow$
  • ${\nabla }_{\theta }\log {\pi }_{\theta }(A_t|S_t)\cdot G_t$ 与 ${\nabla }_{\theta }\log {\pi }_{\theta }(A_t|S_t)$ 方向相反
• 书里边及老师的视频里有非常精彩的论述
  • ${\nabla }_{\theta }\ln \pi (a_t|s_t,{\theta }_t)=\frac{{\nabla }_{\theta }\pi (a_t|s_t,{\theta }_t)}{\pi (a_t|s_t,{\theta }_t)}$
  • $$\begin{array}{rl}{\theta }_{t+1}& ={\theta }_t+\alpha {\nabla }_{\theta }\ln \pi (a_t|s_t,{\theta }_t)q_t(s_t,a_t)\\ & ={\theta }_t+\alpha \underset{{\beta }_t}{\underbrace{\left(\frac{q_t(s_t,a_t)}{\pi (a_t|s_t,{\theta }_t)}\right)}}{\nabla }_{\theta }\pi (a_t|s_t,{\theta }_t).\end{array}$$
  • ${\theta }_{t+1}={\theta }_t+\alpha {\beta }_t{\nabla }_{\theta }\pi (a_t|s_t,{\theta }_t)$
    • ${\beta }_t>0$：梯度上升，提升 $\pi (a_t|s_t,{\theta }_t)$
    • ${\beta }_t<0$：梯度下降，降低 $\pi (a_t|s_t,{\theta }_t)$

4.2 $G_t$的高方差、信用分配问题

• 如果一个完整的回答（一条轨迹 Trajectory）最终获得了很高的总奖励 ，那么就调高这条轨迹中每一步动作（生成每一个 token）的概率。反之，如果总奖励很低，就降低这些动作的概率。它直接使用蒙特卡洛采样得到的累积奖励 Gt 来指导策略更新。
  • Prompt: “法国的首都是哪里？”
    • “法国的首都是巴黎” 奖励模型评估: 这是一个完全正确、简洁的回答。给予高分奖励，比如 +10分。
    • “法国的首都是里昂” 奖励模型评估: 这是一个事实性错误。尽管大部分内容都很好，但核心信息是错的。奖励模型会给予一个很低的惩罚性分数，比如 -10分。
      • {"巴黎": 90%, "里昂": 8%, "马赛": 2%}
    • REINFORCE 的学习规则是：用最终的总奖励，去等同地“奖赏”或“惩罚”这条路上的每一个决策（每一个生成的 token）。
      • 请看 “法国”、“的”、“首都”、“是” 这四个完全正确的、在两个场景中一模一样的 token。
        • 在场景一中，它们的概率被提升了。
        • 在场景二中，它们的概率被降低了。
        • 模型收到了完全相反的训练信号。仅仅因为最后一个词的“运气不好”，导致前面所有正确的努力都被全盘否定。
• 这就是**高方差（High Variance）**的根源。对于模型来说，它完全搞不清楚自己到底做对了什么，做错了什么。它只知道“有时候我这么说会被奖励，有时候会被惩罚，看起来像纯粹的运气”。这种充满噪声和矛盾的梯度信号，使得模型很难稳定地学习到真正有用的知识，训练过程自然会剧烈波动且收敛缓慢。
  • 这就是为什么 PPO 等算法要引入 Critic 网络来学习优势函数 (Advantage Function)。Critic 的作用就像一个更聪明的老师，它不只看总分，还会尝试去评估“在当前情况下，生成这个词比生成其他词好多少”，从而给出更精确、方差更低的指导信号，解决了 REINFORCE 的这个核心缺陷。而 REINFORCE++ 则是通过优势归一化等技巧，在不引入 Critic 的情况下，试图达到类似降低方差的效果。
• 信用分配不公的核心（稀疏 reward 的场景下）：用一个全局的、最终的结果（$G_t$），去评价一系列局部的、具体的行为（$a_t$），导致了“一荣俱荣，一损俱损”的局面。

4.3 TRPO v.s. PPO

4.3.1 on-policy v.s. off-policy

• on-policy 同策略，off-policy 异策略
  • 行为策略（rollout 产生数据的策略），目标策略（待学习的目标策略）；
  • 智能体学习的策略（目标策略）与它用来生成经验数据（行为策略）的策略是同一个。
• 结合策略梯度定义的相关代码分析
  • https://www.datacamp.com/tutorial/policy-gradient-theorem
  • 没有经验回放 (Experience Replay)：代码中没有使用经验回放机制。经验回放通常用于 off-policy 算法，它允许智能体从过去由不同策略（可能是旧版本的策略或完全不同的探索策略）生成的经验中学习。而这里的代码是直接使用当前 episode 产生的数据进行更新。
  • REINFORCE 是一种经典的 on-policy 策略梯度算法。
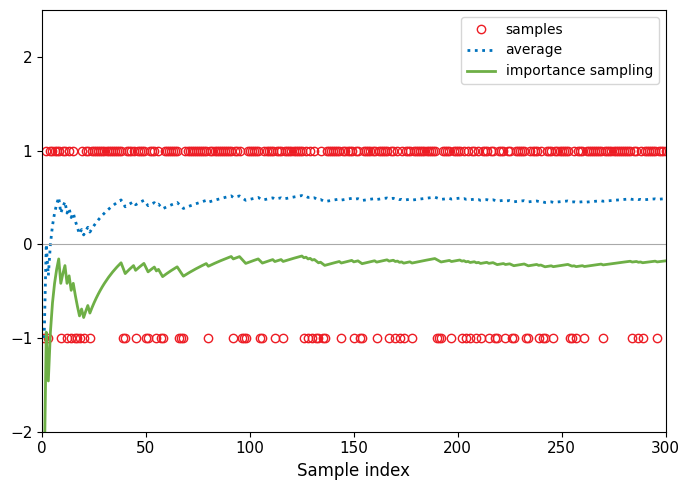
• IS (importance sampling)：ratio 从哪里来的
  $$\begin{array}{rl}{\mathbb{E}}_{x\sim p}[f(x)]& =\int p(x)f(x)dx\\ & =\int q(x)\frac{p(x)}{q(x)}f(x)dx\\ & ={\mathbb{E}}_{x\sim q}\left[\frac{p(x)}{q(x)}f(x)\right]\end{array}$$

# Figure 10.2
import numpy as np
import matplotlib.pyplot as pltN_SAMPLES = 300  # 样本数量
p0_dist = {1: 0.5, -1: 0.5}
p1_dist = {1: 0.8, -1: 0.2}sample_values = np.array([1, -1])
probabilities_p1 = np.array([p1_dist[1], p1_dist[-1]])
generated_samples = np.random.choice(sample_values, size=N_SAMPLES, p=probabilities_p1)sample_indices = np.arange(1, N_SAMPLES + 1)cumulative_mean_p1 = np.cumsum(generated_samples) / sample_indicesimportance_weights = np.zeros(N_SAMPLES)
importance_weights = np.where(generated_samples == 1,p0_dist[1] / p1_dist[1],p0_dist[-1] / p1_dist[-1]
)weighted_samples = generated_samples * importance_weights
cumulative_mean_importance_sampling = np.cumsum(weighted_samples) / sample_indicesplt.figure(figsize=(7, 5)) # 图表尺寸，尽量与原图比例一致color_samples = '#ED1C24'        # 红色 (样本点)
color_average_p1 = '#0072BD'     # 蓝色 (p1平均值)
color_importance = '#6EAF46'     # 绿色 (重要性采样平均值)
color_zeroline = 'darkgrey'      # y=0 参考线颜色plt.plot(sample_indices, generated_samples, 'o',markerfacecolor='none',markeredgecolor=color_samples,markersize=6,label='samples')plt.plot(sample_indices, cumulative_mean_p1,linestyle=':',color=color_average_p1,linewidth=2,label='average')plt.plot(sample_indices, cumulative_mean_importance_sampling,linestyle='-',color=color_importance,linewidth=2,label='importance sampling')plt.axhline(0, color=color_zeroline, linestyle='-', linewidth=0.8)
plt.xlabel('Sample index', fontsize=12)
plt.xlim(0, N_SAMPLES)
plt.ylim(-2, 2.5)
plt.xticks(np.arange(0, N_SAMPLES + 1, 50), fontsize=11)
plt.yticks(np.arange(-2, 3, 1), fontsize=11)
plt.legend(fontsize=10, frameon=True, loc='upper right')plt.tight_layout()

• PG可以知道参数更新的方向，但无法保证更新的步幅

$$\begin{array}{rl}{\text{maximize}}_{\theta }& L_{{\theta }_{old}}(\theta )={\mathbb{E}}_{s\sim {\rho }_{{\theta }_{old}},a\sim {\pi }_{{\theta }_{old}}}\left[\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_{old}}(a|s)}{A}^{{\pi }_{{\theta }_{old}}}(s,a)\right]\\ \text{subject to}& {\mathbb{E}}_{s\sim {\rho }_{{\theta }_{old}}}[D_{KL}({\pi }_{{\theta }_{old}}(\cdot |s)||{\pi }_{\theta }(\cdot |s))]\le \delta \end{array}$$

$$L^{CLIP}(\theta )={\mathbb{E}}_t\left[\min \left(r_t(\theta )A_t^{{\pi }_{{\theta }_{old}}},\text{clip}(r_t(\theta ),1-ϵ,1+ϵ)A_t^{{\pi }_{{\theta }_{old}}}\right)\right]$$

---

5 RL v.s. SFT

在监督学习中，优化过程可以分解为两个核心步骤：

1. 梯度计算：${\nabla }_{\theta }\mathcal{L}(\theta )={\mathbb{E}}_{x\sim \mathcal{D}}[{\nabla }_{\theta }\ell (f_{\theta }(x),y)]$
2. 参数更新：${\theta }_{t+1}={\theta }_t-\alpha {\nabla }_{\theta }\mathcal{L}({\theta }_t)$

其中梯度可以分解为两部分：

• 一阶导函数 $g(x)={\nabla }_{\theta }\ell (f_{\theta }(x),y)$：描述损失函数的局部几何特性
• 数据点 $x$：从固定分布 $\mathcal{D}$ 中采样得到

关键特点：数据分布 $\mathcal{D}$ 是静态的，与参数 $\theta$ 无关。即使步长选择不当，梯度方向通常仍然指向合理的优化方向。

---

强化学习中的 Policy Gradient 方法引入了额外的复杂性：

1. 轨迹采样：$\tau \sim p_{{\pi }_{\theta }}(\tau )=p(s_0){\prod }_{t=0}^{T-1}{\pi }_{\theta }(a_t|s_t)p(s_{t+1}|s_t,a_t)$
2. 梯度估计：${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{\tau \sim p_{{\pi }_{\theta }}(\tau )}[{\sum }_{t=0}^{T-1}{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)A^{{\pi }_{\theta }}(s_t,a_t)]$
3. 参数更新：${\theta }_{t+1}={\theta }_t+\alpha {\nabla }_{\theta }J({\theta }_t)$

与监督学习不同，这里的"数据" $\tau$ 来自于当前策略 ${\pi }_{\theta }$ 与环境的交互。这导致了一个关键的循环依赖：

$$\text{策略质量}\to \text{轨迹质量}\to \text{梯度估计质量}\to \text{策略更新质量}$$

• RL 中的数据是智能体与环境交互的经验；
  • learning from data (learning from interaction)

6 DeepSeekMath Unified Paradigm

$${\nabla }_{\theta }{\mathcal{J}}_{\mathcal{A}}(\theta )=\underset{\text{Data Source}}{\underbrace{\mathbb{E}[(q,o)\sim \mathcal{D}]}}\left(\frac{1}{|o|}\sum _{t=1}^{|o|}\underset{\text{Gradient Coefficient}}{\underbrace{G{C}_{\mathcal{A}}(q,o,t,{\pi }_{rf})}}{\nabla }_{\theta }\log {\pi }_{\theta }(o_t|q,o_{<t})\right)$$

• ${\pi }_{rf}$: reward function

• the gradient coefficient GC that determines the magnitude of the penalty or reinforcement for the data.

• $\log \sigma (\beta R(o^{+})-\beta R(o^{-}))$

  • $R(o)=\frac{1}{|o|}\sum \log \frac{{\pi }_{\theta }}{{\pi }_{ref}}$
  • $\nabla \log \sigma (\Delta )=\frac{\sigma (\Delta )(1-\sigma (\Delta ))}{\sigma (\Delta )}=(1-\sigma (\Delta ))=\sigma (-\Delta )$

• $\nabla {\pi }_{\theta }={\pi }_{\theta }\nabla \log {\pi }_{\theta }$ ($f^{\prime }=f\nabla \log f$)

$$\begin{gathered} {\nabla }_{\theta }{\mathcal{L}}_{\text{DPO}}({\pi }_{\theta },{\pi }_{\text{ref}})= \\ -\beta {\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}\left[\underset{\text{higher weight when reward estimate is wrong}}{\underbrace{\sigma ({\hat{r}}_{\theta }(x,y_{\ell })-{\hat{r}}_{\theta }(x,y_w))}}\left[\underset{\text{increase likelihood of }{y}_w}{\underbrace{{\nabla }_{\theta }\log \pi (y_w|x)}}-\underset{\text{decrease likelihood of }{y}_{\ell }}{\underbrace{{\nabla }_{\theta }\log \pi (y_{\ell }|x)}}\right]\right] \end{gathered}$$

---

PART 2

纳什现在RL4LLM合集里面什么都放了，6.8更了一期RL的内容，这期还是PG的内容

[RL insights] 推导和理解 Policy Gradient 算法，PG vs. MLE/SFT，采样及训练过程

code

参考资料：

• https://rail.eecs.berkeley.edu/deeprlcourse/

强化学习的终极目标：

$$\begin{array}{rl}J(\theta )& =E_{\tau }[R(\tau )]\\ J(\theta )& =E_{\tau \sim p_{\theta }(\tau )}\left[\sum _{t}r(s_t,a_t)\right]\\ {\theta }^{\star }& =\arg \max E_{\tau \sim p_{\theta }(\tau )}\left[\sum _{t}r(s_t,a_t)\right]\\ & =\arg \max \sum _{t=1}^T{E}_{(s_t,a_t)\sim p_{\theta }(s_t,a_t)}[r(s_t,a_t)]\end{array}$$

• 最大化所有可能轨迹对应的回报的期望（an expected value under the trajectory distribution of the sum of rewards）

  • $p_{\theta }(\tau )=p_{\theta }(s_1,a_1,s_2,a_2,\cdots ,s_T,a_T)=p(s_1){\Pi }_{t=1}^T{\pi }_{\theta }(a_t|s_t)p(s_{t+1}|s_t,a_t)$
  • 绝不仅仅只是当前即时的 reward（$r(s,a)$），比如开车开得很快即时的奖励可能很高，但后续可能会有危险（low reward）的结果
  • 期望一定是关于某一概率分布的，这里是关于轨迹（$p_{\theta }(\tau )$）的回报的期望；
  • standard RL objective：无法直接优化，才有了后续的易于优化的 policy gradient，ppo 等
    • 对比看下 soft rl，dpo；
  • ${\sum }_{t=1}^T{E}_{(s_t,a_t)\sim p_{\theta }(s_t,a_t)}[r(s_t,a_t)]$：先对 $r(s_t,a_t)$ 求期望再加和
    • $p(s_{t+1},a_{t+1}|s_t,a_t)=p(s_{t+1}|s_t,a_t){\pi }_{\theta }(a_{t+1}|s_{t+1})$
    • 从“评估无数条完整路径的平均总分”，转变为“评估在每个时间步的平均得分，然后把它们加起来”。

• $J(\theta )=\int P(\tau |\theta )\cdot R(\tau )d\tau$

  • 直接尝试对 RL objective 求导
  • ${\nabla }_{\theta }J(\theta )={\nabla }_{\theta }\int P(\tau |\theta )\cdot R(\tau )d\tau$
  • ${\nabla }_{\theta }J(\theta )=\int [{\nabla }_{\theta }P(\tau |\theta )]\cdot R(\tau )d\tau$
    • 我们没法直接计算 ${\nabla }_{\theta }P(\tau |\theta )$，更重要的是，梯度算子作用在了概率分布 $P(\tau |\theta )$ 上，这使得我们无法通过采样（sampling）来估计这个积分。我们需要把 ${\nabla }_{\theta }$ 从 $P(\tau |\theta )$ 上“挪开”。
      • ${\nabla }_{\theta }P(\tau |\theta )$ 不是概率分布（可正可负，刻画的是 改变策略参数 $\theta$ 时，轨迹 $\tau$ 发生的概率会如何变化）
    • ${\nabla }_{\theta }P(\tau |\theta )=P(\tau |\theta )\cdot {\nabla }_{\theta }\log P(\tau |\theta )$
    • $\nabla f=f\nabla \log f$
  • ${\nabla }_{\theta }J(\theta )=\int P(\tau |\theta )\cdot [R(\tau )\cdot {\nabla }_{\theta }\log P(\tau |\theta )]d\tau$
    • $P(\tau |\theta )$：属于可以被采样的概率分布
    • ${\sum }_t{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)$，这是可以通过策略网络的反向传播计算的
  • ${\nabla }_{\theta }J(\theta )=E_{\tau }[R(\tau )\cdot {\nabla }_{\theta }\log P(\tau |\theta )]$
    • $P(\tau |\theta )=p(s_0)\cdot {\pi }_{\theta }(a_0|s_0)\cdot p(s_1|s_0,a_0)\cdot {\pi }_{\theta }(a_1|s_1)\cdot ...$
    • ${\nabla }_{\theta }\log P(\tau |\theta )={\nabla }_{\theta }[\log p(s_0)+{\sum }_t\log {\pi }_{\theta }(a_t|s_t)+{\sum }_t\log p(s_{t+1}|s_t,a_t)]$
    • 环境的状态转移概率 $p(s_{t+1}|s_t,a_t)$ 和初始状态概率 $p(s_0)$ 都与我们的策略参数 $\theta$ 无关，所以它们的梯度为0。只剩下策略部分：
      • ${\nabla }_{\theta }\log P(\tau |\theta )={\sum }_t{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)$
        $${\nabla }_{\theta }J(\theta )=E_{\tau }[R(\tau )\cdot (\sum _t{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t))]$$

• 整个过程

  • 我们用当前策略 ${\pi }_{\theta }$ 运行 N 次，得到 N 条轨迹 ${\tau }_1,{\tau }_2,...,{\tau }_N$。这等价于从 $P(\tau |\theta )$ 中采样。
    • $J(\theta )=E_{\tau \sim p_{\theta }(\tau )}\left[{\sum }_{t}r({\mathbf{s}}_t,{\mathbf{a}}_t)\right]\approx \frac{1}{N}{\sum }_i{\sum }_{t}r({\mathbf{s}}_{i,t},{\mathbf{a}}_{i,t})$
  • 对于每一条轨迹 ${\tau }_i$，我们计算一个值 $V_i=R({\tau }_i)\cdot {\nabla }_{\theta }\log P({\tau }_i|\theta )$
  • 平均：${\nabla }_{\theta }J(\theta )\approx (1/N)\ast \sum V_i$。
  • 梯度上升

• 两个可以优化的地方

  • 因果性 (Causality)：在 $t$ 时刻的决策，不应该被 $t$ 时刻之前的奖励所影响。所以，对于 $t$ 时刻的策略梯度 ${\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)$，我们只应该乘以它未来的回报 $G_t={\sum }_{k=t}^T{r}_k$(return to go )，而不是整个轨迹的回报 $R(\tau )$。
  • 高方差 (High Variance)：回报值本身波动很大。我们可以减去一个基线 (Baseline) $b(s_t)$ 来减小方差，而不改变梯度的期望值。最常用的基线就是状态价值函数 $V(s_t)$。
  • 经过这两个优化，我们将乘数项从 $R(\tau )$ 变成了 优势函数 (Advantage Function) $A_t=G_t-V(s_t)$。

	变换前 (Problematic Form)	变换后 (Solvable Form)
积分形式	∫ [∇_θ P(τ|θ)] * R(τ) dτ	∫ P(τ|θ) * [R(τ) * ∇_θ log P(τ|θ)] dτ
采样分布	∇_θ P(τ|θ) (不是概率分布, 无法采样)	P(τ|θ) (是概率分布, 可以采样)
待求值的函数	R(τ)	R(τ) * ∇_θ log P(τ|θ)
可行性	无法通过蒙特卡洛方法估算	可以通过蒙特卡洛方法估算

我们精心设计一个损失函数 L(θ)，使得最小化 L(θ) 的效果等同于最大化 J(θ)。

$$L(\theta )=-E[\sum _t(\log {\pi }_{\theta }(a_t|s_t)\cdot G_t)]$$

• ${\nabla }_{\theta }L(\theta )=-{\nabla }_{\theta }J(\theta )$

  • ${\nabla }_{\theta }L(\theta )$: loss.backward()

• 在很多优化问题中，我们真正想优化的“原始目标”（True Objective）往往很难处理（比如包含期望、不可微等）。因此，我们会构造一个更容易处理的**“代理目标” (Surrogate Objective)**。我们对代理目标的要求是：优化这个代理目标，能够保证我们的原始目标也得到改善。

  • ppo-clip 也是一种代理目标；

• pg vs. mle (sft)

  • mle：一视同仁增加所有动作的概率（专家数据，无负样本）
  • pg：根据奖励值进行增加或减少，高回报 trajectory 的 log p 会提升，低回报 trajectory 的 log p 会降低
    • weighted version of mle